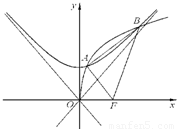
题目内容
设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线 与
与 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.(1)求双曲线C2的标准方程;
(2)若C1与C2在第一象限内有两个公共点A和B,求p的取值范围,并求
 的最大值;
的最大值;(3)是否存在正数p,使得此时△FAB的重心G恰好在双曲线C2的渐近线上?如果存在,求出p的值;如果不存在,说明理由.

【答案】分析:(1)设双曲线C2的方程,利用C2是以直线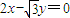 与
与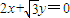 为渐近线,焦点是
为渐近线,焦点是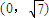 ,即可求得双曲线方程;
,即可求得双曲线方程;
(2)抛物线方程与双曲线方程联立,可得一元二次方程,利用C1与C2在第一象限内有两个公共点A和B,可得p的取值范围;设A、B的坐标,用坐标表示 ,利用韦达定理及配方法,可得
,利用韦达定理及配方法,可得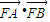 的最大值;
的最大值;
(3)由(2)知△FAB的重心G(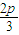 ,
,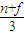 ),即G(
),即G(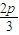 ,
,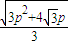 ),假设G恰好在双曲线C2的渐近线上,利用渐近线方程,即可求得结论.
),假设G恰好在双曲线C2的渐近线上,利用渐近线方程,即可求得结论.
解答:解:(1)因为一个焦点是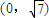 ,故焦点在y轴上,于是可设双曲线C2的方程为
,故焦点在y轴上,于是可设双曲线C2的方程为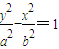 (a>0,b>0)
(a>0,b>0)
∵C2是以直线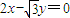 与
与 为渐近线,
为渐近线,
∴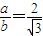
∵a2+b2=7
∴a=2,b=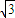
∴双曲线方程为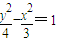 ;
;
(2)抛物线y2=2px(p>0)的焦点F(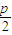 ,0),与双曲线方程联立消y得:4x2-6px+12=0
,0),与双曲线方程联立消y得:4x2-6px+12=0
∵C1与C2在第一象限内有两个公共点A和B,∴△>0,∴p>
设A(m,n)、B(e,f),则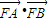 =(m-
=(m-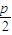 ,n)•(e-
,n)•(e-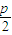 ,f)=me-(m+e)×
,f)=me-(m+e)× +
+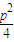 +nf=me-(m+e)×
+nf=me-(m+e)×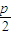 +
+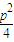 +2p
+2p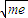
由方程知me=3,m+e=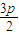 代入得
代入得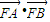 =-
=-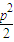 +2
+2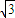 p+3=-
p+3=- (p-2
(p-2 )2+9,函数的对称轴为p=2
)2+9,函数的对称轴为p=2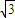
∵p>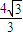 ,∴p=2
,∴p=2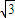 时,
时,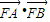 的最大值为9;
的最大值为9;
(3)由(2)知△FAB的重心G( ,
, )
)
∵n+f=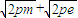 =
=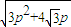
∴G(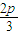 ,
,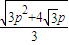 )
)
假设G恰好在双曲线C2的渐近线上,则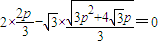 ,∴
,∴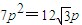
∴p=0或p=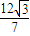
∵p>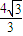 ,∴p=
,∴p=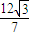
∴存在正数p= ,使得此时△FAB的重心G恰好在双曲线C2的渐近线上.
,使得此时△FAB的重心G恰好在双曲线C2的渐近线上.
点评:本题考查双曲线的标准方程,考查向量知识的运用,考查函数的最值,考查学生分析解决问题的能力,属于中档题.
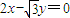 与
与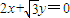 为渐近线,焦点是
为渐近线,焦点是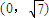 ,即可求得双曲线方程;
,即可求得双曲线方程;(2)抛物线方程与双曲线方程联立,可得一元二次方程,利用C1与C2在第一象限内有两个公共点A和B,可得p的取值范围;设A、B的坐标,用坐标表示
 ,利用韦达定理及配方法,可得
,利用韦达定理及配方法,可得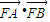 的最大值;
的最大值;(3)由(2)知△FAB的重心G(
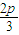 ,
,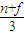 ),即G(
),即G(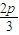 ,
,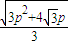 ),假设G恰好在双曲线C2的渐近线上,利用渐近线方程,即可求得结论.
),假设G恰好在双曲线C2的渐近线上,利用渐近线方程,即可求得结论.解答:解:(1)因为一个焦点是
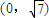 ,故焦点在y轴上,于是可设双曲线C2的方程为
,故焦点在y轴上,于是可设双曲线C2的方程为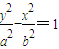 (a>0,b>0)
(a>0,b>0)∵C2是以直线
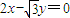 与
与 为渐近线,
为渐近线,∴
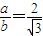
∵a2+b2=7
∴a=2,b=
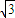
∴双曲线方程为
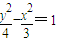 ;
;(2)抛物线y2=2px(p>0)的焦点F(
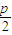 ,0),与双曲线方程联立消y得:4x2-6px+12=0
,0),与双曲线方程联立消y得:4x2-6px+12=0∵C1与C2在第一象限内有两个公共点A和B,∴△>0,∴p>

设A(m,n)、B(e,f),则
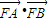 =(m-
=(m-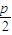 ,n)•(e-
,n)•(e-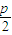 ,f)=me-(m+e)×
,f)=me-(m+e)× +
+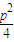 +nf=me-(m+e)×
+nf=me-(m+e)×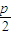 +
+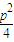 +2p
+2p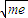
由方程知me=3,m+e=
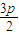 代入得
代入得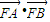 =-
=-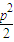 +2
+2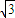 p+3=-
p+3=- (p-2
(p-2 )2+9,函数的对称轴为p=2
)2+9,函数的对称轴为p=2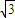
∵p>
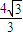 ,∴p=2
,∴p=2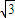 时,
时,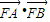 的最大值为9;
的最大值为9;(3)由(2)知△FAB的重心G(
 ,
, )
)∵n+f=
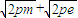 =
=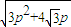
∴G(
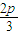 ,
,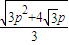 )
)假设G恰好在双曲线C2的渐近线上,则
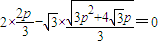 ,∴
,∴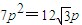
∴p=0或p=
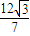
∵p>
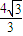 ,∴p=
,∴p=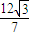
∴存在正数p=
 ,使得此时△FAB的重心G恰好在双曲线C2的渐近线上.
,使得此时△FAB的重心G恰好在双曲线C2的渐近线上.点评:本题考查双曲线的标准方程,考查向量知识的运用,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 (2012•上海模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线
(2012•上海模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线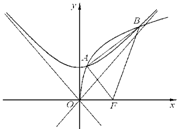 (2012•贵阳模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线
(2012•贵阳模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线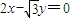 与
与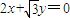 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.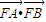 的最大值;
的最大值; 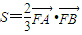 ,求p的值.
,求p的值.
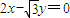 与
与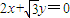 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.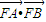 的最大值;
的最大值; 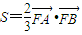 ,求p的值.
,求p的值.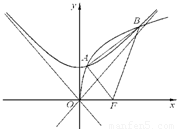
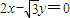 与
与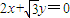 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.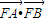 的最大值;
的最大值; 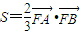 ,求p的值.
,求p的值.