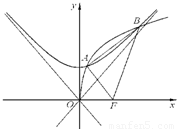
题目内容
设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线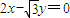 与
与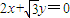 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.(1)求双曲线C2的标准方程;
(2)若C1与C2在第一象限内有两个公共点A和B,求p的取值范围,并求
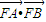 的最大值;
的最大值; (3)若△FAB的面积S满足
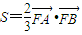 ,求p的值.
,求p的值.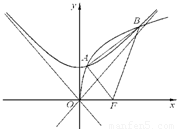
【答案】分析:(1)设双曲线C2的标准方程,利用C2是以直线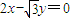 与
与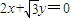 为渐近线,以
为渐近线,以 为一个焦点的双曲线,及a2+b2=c2,即可求得双曲线C2的标准方程;
为一个焦点的双曲线,及a2+b2=c2,即可求得双曲线C2的标准方程;
(2)将抛物线y2=2px代入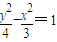 ,整理可得2x2-3px+6=0,根据C1与C2在第一象限内有两个公共点A和B,即可确定p的取值范围,从而求出
,整理可得2x2-3px+6=0,根据C1与C2在第一象限内有两个公共点A和B,即可确定p的取值范围,从而求出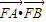 的最大值;
的最大值;
(3)直线AB的方程为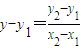 (x-x1),求出F到直线AB的距离,从而可求面积S,根据
(x-x1),求出F到直线AB的距离,从而可求面积S,根据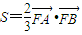 ,建立方程,即可求得结论.
,建立方程,即可求得结论.
解答:解:(1)设双曲线C2的标准方程为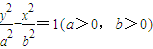
∵C2是以直线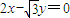 与
与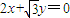 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.
∴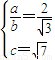 ,
,
∵a2+b2=c2,
∴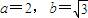
∴双曲线C2的标准方程为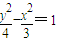 ;
;
(2)将抛物线y2=2px代入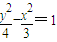 ,整理可得2x2-3px+6=0
,整理可得2x2-3px+6=0
设A(x1,y1),B(x2,y2)(x1>0,y1>0,x2>0,y2>0),则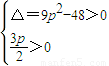
∴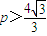
∵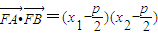 +y1y2=
+y1y2=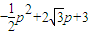 =
=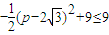
∴当且仅当p=2 时,
时,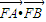 的最大值为9;
的最大值为9;
(3)直线AB的方程为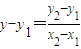 (x-x1),即
(x-x1),即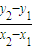 x-y-
x-y-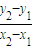 ×x1+y1=0
×x1+y1=0
∴F到直线AB的距离为d=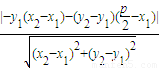
∴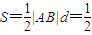
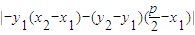 =
=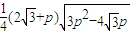
∵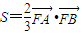 ,
,
∴ (
(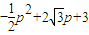 )=
)=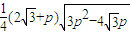
∴p=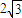 .
.
点评:本题考查双曲线的标准方程,考查抛物线与双曲线的位置关系,考查三角形面积的计算,综合性强,难度大.
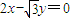 与
与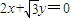 为渐近线,以
为渐近线,以 为一个焦点的双曲线,及a2+b2=c2,即可求得双曲线C2的标准方程;
为一个焦点的双曲线,及a2+b2=c2,即可求得双曲线C2的标准方程;(2)将抛物线y2=2px代入
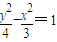 ,整理可得2x2-3px+6=0,根据C1与C2在第一象限内有两个公共点A和B,即可确定p的取值范围,从而求出
,整理可得2x2-3px+6=0,根据C1与C2在第一象限内有两个公共点A和B,即可确定p的取值范围,从而求出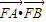 的最大值;
的最大值; (3)直线AB的方程为
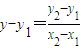 (x-x1),求出F到直线AB的距离,从而可求面积S,根据
(x-x1),求出F到直线AB的距离,从而可求面积S,根据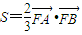 ,建立方程,即可求得结论.
,建立方程,即可求得结论.解答:解:(1)设双曲线C2的标准方程为
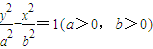
∵C2是以直线
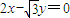 与
与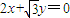 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.∴
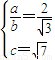 ,
,∵a2+b2=c2,
∴
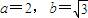
∴双曲线C2的标准方程为
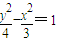 ;
;(2)将抛物线y2=2px代入
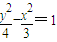 ,整理可得2x2-3px+6=0
,整理可得2x2-3px+6=0设A(x1,y1),B(x2,y2)(x1>0,y1>0,x2>0,y2>0),则
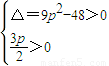
∴
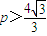
∵
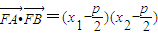 +y1y2=
+y1y2=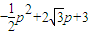 =
=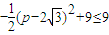
∴当且仅当p=2
 时,
时,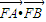 的最大值为9;
的最大值为9;(3)直线AB的方程为
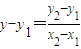 (x-x1),即
(x-x1),即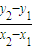 x-y-
x-y-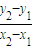 ×x1+y1=0
×x1+y1=0∴F到直线AB的距离为d=
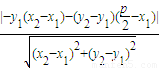
∴
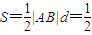
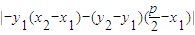 =
=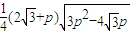
∵
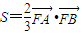 ,
,∴
 (
(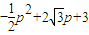 )=
)=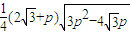
∴p=
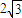 .
.点评:本题考查双曲线的标准方程,考查抛物线与双曲线的位置关系,考查三角形面积的计算,综合性强,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•上海模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线
(2012•上海模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线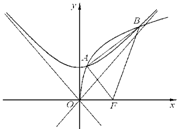 (2012•贵阳模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线
(2012•贵阳模拟)设C1是以F为焦点的抛物线y2=2px(p>0),C2是以直线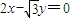 与
与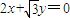 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.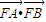 的最大值;
的最大值; 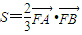 ,求p的值.
,求p的值.
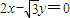 与
与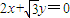 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.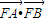 的最大值;
的最大值; 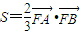 ,求p的值.
,求p的值.