题目内容
(本小题满分12分)
已知数列 ,且
,且 是函数
是函数 ,(
,( )的一个极值点.数列
)的一个极值点.数列 中
中 (
( 且
且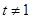 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)记 ,当
,当 时,数列
时,数列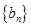 的前
的前 项和为
项和为 ,求使
,求使 的
的 的最小值;
的最小值;
(3)若 ,证明:
,证明: (
( )。
)。
【答案】
(1) 。
。
(2)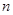 的最小值为1006.
的最小值为1006.
(3)略
【解析】解:(1)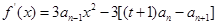 ,
,
所以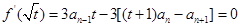 ,整理得
,整理得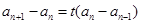
当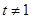 时,
时,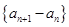 是以
是以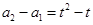 为首项,
为首项,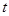 为公比的等比数列,
为公比的等比数列,
所以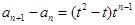
方法一:由上式得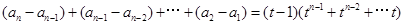
所以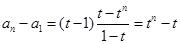 ,所以
,所以 。
。
当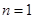 时上式仍然成立,故
时上式仍然成立,故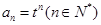 ……………4分
……………4分
方法二:由上式得: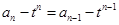 ,所以
,所以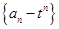 是常数列,
是常数列,
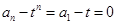 ,
, 。
。
又,当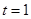 时上式仍然成立,故
时上式仍然成立,故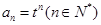
(2)当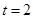 时,
时,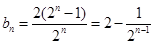
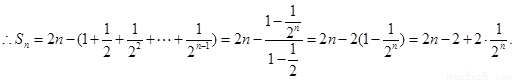
由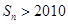 ,得
,得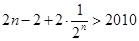 ,
,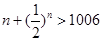 ,
,
当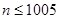 时,
时,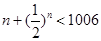 ,当
,当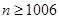 时,
时,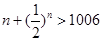
因此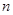 的最小值为1006.……………8分
的最小值为1006.……………8分
(3)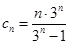 ,
,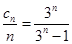 ,所以证明
,所以证明 ,
,
即证明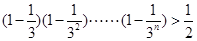
因为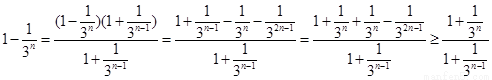 ,
,
所以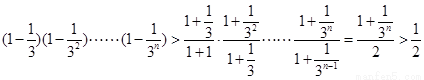 ,从而原命题得证………12分
,从而原命题得证………12分

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目