题目内容
已知命题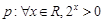 ,那么命题
,那么命题 为
为
A. | B. |
C. | D. |
C
解析试题分析:全称命题的否定是特称命题,直接写出¬p即可.
∵“全称命题”的否定一定是“存在性命题”,
∴命题 p:?x∈R,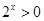 ,那么命题¬p:?x∈R,
,那么命题¬p:?x∈R,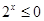 .
.
故选C
考点:全称命题
点评:命题的否定即命题的对立面.“全称量词”与“存在量词”正好构成了意义相反的表述.基本知识的考查.

练习册系列答案
相关题目
“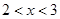 ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
原命题:“设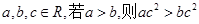 ”以及它的逆命题、否命题、逆否命题中,真命题共有( )个.
”以及它的逆命题、否命题、逆否命题中,真命题共有( )个.
| A.0 | B.1 | C.2 | D.4 |
若函数 在
在 处有定义,则“
处有定义,则“ 在
在 处取得极值”是“
处取得极值”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列说法错误的是( )
A.命题“若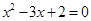 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若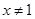 ,则 ,则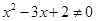 ” ” |
B.“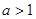 ”是“ ”是“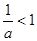 ”的充分不必要条件 ”的充分不必要条件 |
C.若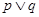 为真命题,则 为真命题,则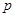 、 、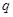 均为真命题 均为真命题 |
D.若命题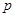 :“存在 :“存在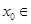 R, R,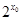 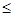 0”,则 0”,则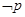 :“对任意的 :“对任意的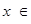 R, R,  >0”. >0”. |
若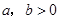 ,则
,则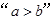 是“
是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
已知命题 ,则
,则 是 ( )
是 ( )
A. | B.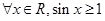 |
C.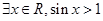 | D.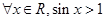 |
命题“若α= ,则tanα=1”的逆否命题是
,则tanα=1”的逆否命题是
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,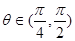 ,
,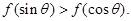
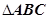 中,
中,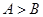 是
是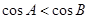 的充要条件.
的充要条件. 为非零向量,且
为非零向量,且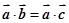 ,则
,则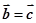 .
.