题目内容
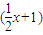 10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,其中ak (k=0,1,2,…,9,10)都是常数,则a1+2a2+3a3+…+9a9+10a10= .
10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,其中ak (k=0,1,2,…,9,10)都是常数,则a1+2a2+3a3+…+9a9+10a10= .
【答案】分析:首先将 10变形为(
10变形为( )10[1+(x+1)]10,再利用二项式定理展开可得
)10[1+(x+1)]10,再利用二项式定理展开可得 10=(
10=( )10+(
)10+( )10C101(1+x)1+(
)10C101(1+x)1+( )10C102(1+x)2+…+(
)10C102(1+x)2+…+( )10C1010(1+x)10;结合题意,可得a1=(
)10C1010(1+x)10;结合题意,可得a1=( )10C101,a2=(
)10C101,a2=( )10C102,…a10=(
)10C102,…a10=( )10C1010,进而可得a1+2a2+3a3+…+9a9+10a10=(
)10C1010,进而可得a1+2a2+3a3+…+9a9+10a10=( )10C101+(
)10C101+( )10C102+…(
)10C102+…( )10C1010=(
)10C1010=( )10[C101+2C102+…+10C1010],由二项式系数的性质,可得a1+2a2+3a3+…+9a9+10a10=(
)10[C101+2C102+…+10C1010],由二项式系数的性质,可得a1+2a2+3a3+…+9a9+10a10=( )10×10×[C9+C91+…+C99]=(
)10×10×[C9+C91+…+C99]=( )10×10×29,计算可得答案.
)10×10×29,计算可得答案.
解答:解: 10=(
10=( )10[1+(x+1)]10=(
)10[1+(x+1)]10=( )10+(
)10+( )10C101(1+x)1+(
)10C101(1+x)1+( )10C102(1+x)2+…+(
)10C102(1+x)2+…+( )10C1010(1+x)10;
)10C1010(1+x)10;
根据题意,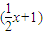 10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,
10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,
则a=( )10,a1=(
)10,a1=( )10C101,a2=(
)10C101,a2=( )10C102,…a10=(
)10C102,…a10=( )10C1010,
)10C1010,
则a1+2a2+3a3+…+9a9+10a10=( )10C101+2(
)10C101+2( )10C102+…+10(
)10C102+…+10( )10C1010,
)10C1010,
=( )10[C101+2C102+…+10C1010],
)10[C101+2C102+…+10C1010],
又由mCnm=nCn-1m-1,则C101=10C9,2C102=10C91,…,10C1010=10C99,
即a1+2a2+3a3+…+9a9+10a10=( )10×10×[C9+C91+…+C99]=(
)10×10×[C9+C91+…+C99]=( )10×10×29=5;
)10×10×29=5;
故答案为5.
点评:本题考查二项式定理的运用,解题的关键要灵活运用二项式系数的性质.
 10变形为(
10变形为( )10[1+(x+1)]10,再利用二项式定理展开可得
)10[1+(x+1)]10,再利用二项式定理展开可得 10=(
10=( )10+(
)10+( )10C101(1+x)1+(
)10C101(1+x)1+( )10C102(1+x)2+…+(
)10C102(1+x)2+…+( )10C1010(1+x)10;结合题意,可得a1=(
)10C1010(1+x)10;结合题意,可得a1=( )10C101,a2=(
)10C101,a2=( )10C102,…a10=(
)10C102,…a10=( )10C1010,进而可得a1+2a2+3a3+…+9a9+10a10=(
)10C1010,进而可得a1+2a2+3a3+…+9a9+10a10=( )10C101+(
)10C101+( )10C102+…(
)10C102+…( )10C1010=(
)10C1010=( )10[C101+2C102+…+10C1010],由二项式系数的性质,可得a1+2a2+3a3+…+9a9+10a10=(
)10[C101+2C102+…+10C1010],由二项式系数的性质,可得a1+2a2+3a3+…+9a9+10a10=( )10×10×[C9+C91+…+C99]=(
)10×10×[C9+C91+…+C99]=( )10×10×29,计算可得答案.
)10×10×29,计算可得答案.解答:解:
 10=(
10=( )10[1+(x+1)]10=(
)10[1+(x+1)]10=( )10+(
)10+( )10C101(1+x)1+(
)10C101(1+x)1+( )10C102(1+x)2+…+(
)10C102(1+x)2+…+( )10C1010(1+x)10;
)10C1010(1+x)10;根据题意,
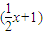 10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,
10=a+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,则a=(
 )10,a1=(
)10,a1=( )10C101,a2=(
)10C101,a2=( )10C102,…a10=(
)10C102,…a10=( )10C1010,
)10C1010,则a1+2a2+3a3+…+9a9+10a10=(
 )10C101+2(
)10C101+2( )10C102+…+10(
)10C102+…+10( )10C1010,
)10C1010,=(
 )10[C101+2C102+…+10C1010],
)10[C101+2C102+…+10C1010],又由mCnm=nCn-1m-1,则C101=10C9,2C102=10C91,…,10C1010=10C99,
即a1+2a2+3a3+…+9a9+10a10=(
 )10×10×[C9+C91+…+C99]=(
)10×10×[C9+C91+…+C99]=( )10×10×29=5;
)10×10×29=5;故答案为5.
点评:本题考查二项式定理的运用,解题的关键要灵活运用二项式系数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目