题目内容
19.设随机变量X的分布函数为F(x)=$\left\{\begin{array}{l}{0(x<-1)}\\{\frac{1}{8}(x=-1)}\\{ax+b(-1<x<1)}\\{1(x≥1)}\end{array}\right.$,又P{-1<X<1}=$\frac{5}{8}$,试确定实数a,b的值.分析 由已知得F(x)是连续函数,从而F(-1)=$\underset{lim}{x→-{1}^{+}}$F(x)=-a+b=$\frac{1}{8}$,F(1)=$\underset{lim}{x→{1}^{-1}}$F(x)=a+b=1,由此能求出实数a,b的值.
解答 解:∵随机变量X的分布函数为F(x)=$\left\{\begin{array}{l}{0(x<-1)}\\{\frac{1}{8}(x=-1)}\\{ax+b(-1<x<1)}\\{1(x≥1)}\end{array}\right.$,又P{-1<X<1}=$\frac{5}{8}$,
∴F(x)是连续函数,
∴F(-1)=$\underset{lim}{x→-{1}^{+}}$F(x)=-a+b=$\frac{1}{8}$,
F(1)=$\underset{lim}{x→{1}^{-1}}$F(x)=a+b=1,
解方程组$\left\{\begin{array}{l}{-a+b=\frac{1}{8}}\\{a+b=1}\end{array}\right.$,得a=$\frac{7}{16}$,b=$\frac{9}{16}$.
点评 本题考查实数值的求法,是基础题,解题时要认真连续型随机变量概率分布函数的性质的合理运用.

练习册系列答案
相关题目
11.若存在非零实数x,y,使不等式(6a-1)x2-2xy+ay2≥0成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (-∞-$\frac{1}{3}$)∪($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{3}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
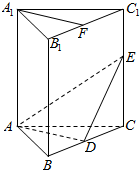 如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.
如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.