题目内容
8.己知函数f(x)=-2a•4x+2x-1.(1)a=1时,求f(x)在[-3,0]的值域;
(2)方程f(x)=0有负根,求a的范围.
分析 (1)当a=1时,f(x)=-2•4x+2x-1=-2(2x-$\frac{1}{4}$)2-$\frac{7}{8}$,从而求值域;
(2)由-2a•4x+2x-1=0知a=-$\frac{1}{2}$(2-x)2+$\frac{1}{2}$•2-x=-$\frac{1}{2}$(2-x-$\frac{1}{2}$)2+$\frac{1}{8}$,从而确定a的范围.
解答 解:(1)当a=1时,
f(x)=-2•4x+2x-1=-2(2x-$\frac{1}{4}$)2-$\frac{7}{8}$,
∵x∈[-3,0],∴2x∈[$\frac{1}{8}$,1],
∴-2≤f(x)≤-$\frac{7}{8}$;
故f(x)在[-3,0]的值域为[-2,-$\frac{7}{8}$];
(2)∵-2a•4x+2x-1=0,
∴a=-$\frac{1}{2}$(2-x)2+$\frac{1}{2}$•2-x=-$\frac{1}{2}$(2-x-$\frac{1}{2}$)2+$\frac{1}{8}$,
∵2-x>1,∴-$\frac{1}{2}$(2-x-$\frac{1}{2}$)2+$\frac{1}{8}$<0;
故a的范围为(-∞,0).
点评 本题考查了函数的值域的求法及复合函数的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.设A是△ABC的一个内角,且sinA=$\frac{\sqrt{3}}{2}$,那么角A等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | kπ+$\frac{π}{3}$(k∈Z) |
4.圆C1:x2+y2+2x+4y-4=0与圆C2:(x-2)2+(y-2)2=4的位置关系为( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
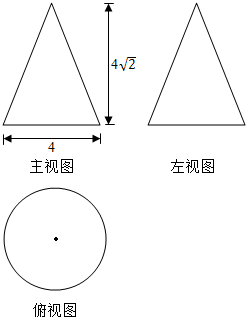 一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.
一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.