题目内容
9.A、B两点的坐标分别为(5,4)、(1,8),P是x2+y2=5上一动点,求S=PA2+PB2最大值和最小值.分析 设P(x,y),则S=PA2+PB2=(x-5)2+(y-4)2+(x-1)2+(y-8)2=-12x-24y+116,利用三角换元,即可得出结论.
解答 解:设P(x,y),则
S=PA2+PB2=(x-5)2+(y-4)2+(x-1)2+(y-8)2=-12x-24y+116,
设x=$\sqrt{5}$cosα,y=$\sqrt{5}$sinα,
∴S=-12$\sqrt{5}$cosα-24$\sqrt{5}$sinα+116=-60sin(α+θ)+116,
∴S=PA2+PB2最大值为176,最小值为56.
点评 本题考查点与圆的位置关系,考查两点间距离公式的运用,考查三角函数知识,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.设A是△ABC的一个内角,且sinA=$\frac{\sqrt{3}}{2}$,那么角A等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | kπ+$\frac{π}{3}$(k∈Z) |
4.圆C1:x2+y2+2x+4y-4=0与圆C2:(x-2)2+(y-2)2=4的位置关系为( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
5.下列计算正确的是( )
| A. | (a3)2=a9 | B. | log26-log23=1 | C. | a${\;}^{-\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=0 | D. | log3(-4)2=2log3(-4) |
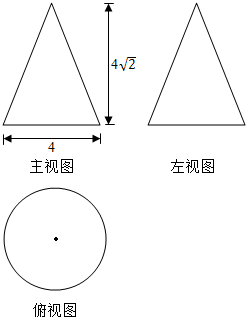 一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.
一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.