题目内容
下列命题正确的个数为 ( )
①已知-1≤x+y≤1,1≤x-y≤3,则3x-y的范围是[1,7];
②若不等式2x-1>m(x2-1)对满足|m|≤2的所有m都成立,则x的范围是(
,
);
③如果正数a,b满足ab=a+b+3,则ab的取值范围是[8,+∞)
④a=log
2,b=log
3,c=(
)0.5大小关系是a>b>c.
①已知-1≤x+y≤1,1≤x-y≤3,则3x-y的范围是[1,7];
②若不等式2x-1>m(x2-1)对满足|m|≤2的所有m都成立,则x的范围是(
| ||
| 2 |
| ||
| 2 |
③如果正数a,b满足ab=a+b+3,则ab的取值范围是[8,+∞)
④a=log
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
分析:①借助线性规划的知识可解得;②变m为主元,利用恒成立可求得x的范围;③借助基本不等式可得ab的范围;④借助指对数函数的单调性可判断大小.
解答:解:①令3x-y=z,作出可行域和直线l:y=3x,
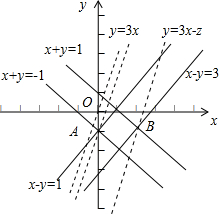
可知当直线y=3x-z过点A(0,-1)(直线x+y=-1与x-y=1的交点)时,z有最小值1,当直线过点B(2,-1)(直线x-y=3与直线x+y=1的交点)时,z有最大值7,
故3x-y的范围是[1,7],故①正确;
②原不等式可整理为(x2-1)m-2x+1>0,令f(m)=(x2-1)m-2x+1,
∵不等式2x-1>m(x2-1)对满足|m|≤2的所有m都成立
∴
,解得
,即
<x<
,故②错误;
③∵正数a,b且满足ab=a+b+3,
∴ab=a+b+3≥2
+3,
∴(
-1)2≥4,
∴
-1≤-2(舍),或
-1≥2,
∴ab≥9,即ab的范围是[9,+∞),故③错误;
④因为对数的底数小于1,而真数大于1,故对数值为负,即a<0,b<0,由指数函数可知c>0,故④错误.
故正确答案为:①.
故选A.

可知当直线y=3x-z过点A(0,-1)(直线x+y=-1与x-y=1的交点)时,z有最小值1,当直线过点B(2,-1)(直线x-y=3与直线x+y=1的交点)时,z有最大值7,
故3x-y的范围是[1,7],故①正确;
②原不等式可整理为(x2-1)m-2x+1>0,令f(m)=(x2-1)m-2x+1,
∵不等式2x-1>m(x2-1)对满足|m|≤2的所有m都成立
∴
|
|
-1-
| ||
| 2 |
1-
| ||
| 2 |
③∵正数a,b且满足ab=a+b+3,
∴ab=a+b+3≥2
| ab |
∴(
| ab |
∴
| ab |
| ab |
∴ab≥9,即ab的范围是[9,+∞),故③错误;
④因为对数的底数小于1,而真数大于1,故对数值为负,即a<0,b<0,由指数函数可知c>0,故④错误.
故正确答案为:①.
故选A.
点评:本题主要考查了命题真假的判断,涉及线性规划的知识、不等式的恒成立中参数范围的求解、基本不等式、指对数函数的性质等,属综合题.解题中要注意常规解题方法的使用与总结,属于中档题.

练习册系列答案
相关题目
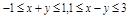 ,则
,则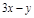 的范围是
的范围是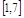 ;
;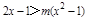 对满足
对满足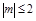 的所有m都成立,则x的范围是
的所有m都成立,则x的范围是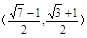 ;
;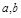 满足
满足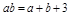 ,则
,则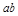 的取值范围是
的取值范围是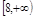
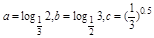 大小关系是
大小关系是