题目内容
若tanα=2,则tan(
+α)的值为
| π | 4 |
-3
-3
.分析:把所求的式子利用两角和与差的正切函数公式及特殊角的三角函数值化简后,将tanα的值代入即可求出值.
解答:解:∵tanα=2,
∴tan(
+α)=
=
=
=-3.
故答案为:-3
∴tan(
| π |
| 4 |
tan
| ||
1-tan
|
=
| 1+tanα |
| 1-tanα |
| 1+2 |
| 1-2 |
故答案为:-3
点评:此题考查了两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +1<0. .
+1<0. .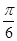 和sinθ=
和sinθ=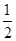 ; ②θ=
; ②θ=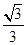 ; ③ρ2-9=0和ρ= 3;
; ③ρ2-9=0和ρ= 3;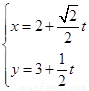 和
和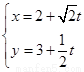 . 其中表示相同曲线的组数为 .
. 其中表示相同曲线的组数为 .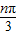 ,n=1,2,3,…
,n=1,2,3,… ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.