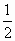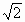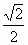题目内容
若(x,y)与(ρ,θ)(ρ∈R)分别是点M的直角坐标和极坐标,t表示参数,则下列各组曲线:
①θ=
和sinθ=
;
②θ=
和tanθ=
;
③ρ2-9=0和ρ=3;
④
和
.
其中表示相同曲线的组数为 .
①θ=
| n |
| 6 |
| 1 |
| 2 |
②θ=
| n |
| 6 |
| ||
| 3 |
③ρ2-9=0和ρ=3;
④
|
|
其中表示相同曲线的组数为
分析:利用极坐标方程将它们化成直角坐标方程后进行判断,或将参数方程消去参数化成直角坐标方程后进行判断即可.
解答:解:①sinθ=
?θ=
+2kπ,或θ=
+2kπ,k∈Z,
它与θ=
不表示相同曲线;
②tanθ=
?θ=
+kπk∈Z,
它与θ=
表示相同曲线;
③ρ2-9=0?ρ=3或ρ=-3,它与ρ=3表示相同曲线;
④
和
化成直角坐标方程分别为y-3=
(x-2)和y-3=
(x-2),
故它们不表示相同曲线.
故答案为:2.
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
它与θ=
| π |
| 6 |
②tanθ=
| ||
| 3 |
| π |
| 6 |
它与θ=
| π |
| 6 |
③ρ2-9=0?ρ=3或ρ=-3,它与ρ=3表示相同曲线;
④
|
|
| ||
| 2 |
| ||
| 4 |
故它们不表示相同曲线.
故答案为:2.
点评:本题考查把极坐标方程、参数方程化为直角坐标方程的方法,属于容易题.

练习册系列答案
相关题目
若直线
x+y=m与圆 (m>0)相切,则m为
(m>0)相切,则m为
[
]|
A . |
B .2 |
C . |
D . |
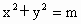 (m>0)相切,则m为
(m>0)相切,则m为