题目内容
观察数列:①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
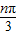 ,n=1,2,3,…
,n=1,2,3,…(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
 ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
【答案】分析:(1)根据所给数据发现他们呈周期性变化,类比周期函数可得周期数列定义
(2)根据递推关系an+2=an+1-an可用做差发求得an+6=-an+3=an,而ak+ak+1+-----+ak+5=0,k∈N*利用周期性知S2008=a1+a2+a3+a4=a2+a3=1007
(3)直接做比较困难,可以利用数学归纳法进行求解
解答:解:(1)存在正整数T,使an+T=an;
(2)证明:由an+2=an+1-an⇒an+3=an+2-an+1=an+1-an-an+1=-an⇒an+6=-an+3=an
所以数列,{an}是以T=6为周期的周期数列
由S2=2008,S3=2010,a1+a2=2008,a1+a2+a3=2010⇒a3=2
于是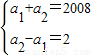 ?
?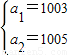
又ak+ak+1+-----+ak+5=0,k∈N*,
所以,S2008=a1+a2+a3+a4=a2+a3=1007
(3)当p=0时,{an}是周期数列,
因为此时an=0(n∈N*)为常数列,
所以对任意给定的正整数T及任意正整数n,
都有an+T=an,符合周期数列的定义.
当p∈(0, )时,{an}是递增数列,不是周期数列.
)时,{an}是递增数列,不是周期数列.
下面用数学归纳法进行证明:
①当n=1时,因为a1=p,p∈(0, )
)
所以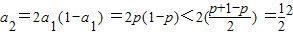 ,
,
且a2-a1=2a1(1-a1)-a1=a1(1-2a1)=p(1-2p)>0
所以a1<a2,a2∈(0, )
)
②假设当n=k时,结论成立,即a1<a2<---<ak,ak∈(0, ),
),
则ak+1-ak=2ak(1-ak)-ak=ak(1-2ak)>0即ak<ak+1
所以当n=k+1时,结论也成立.
根据①、②可知,{an}是递增数列,不是周期数列.
点评:本题考查了周期函数类比到周期数列,研究周期数列的有关问题.
(2)根据递推关系an+2=an+1-an可用做差发求得an+6=-an+3=an,而ak+ak+1+-----+ak+5=0,k∈N*利用周期性知S2008=a1+a2+a3+a4=a2+a3=1007
(3)直接做比较困难,可以利用数学归纳法进行求解
解答:解:(1)存在正整数T,使an+T=an;
(2)证明:由an+2=an+1-an⇒an+3=an+2-an+1=an+1-an-an+1=-an⇒an+6=-an+3=an
所以数列,{an}是以T=6为周期的周期数列
由S2=2008,S3=2010,a1+a2=2008,a1+a2+a3=2010⇒a3=2
于是
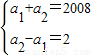 ?
?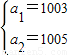
又ak+ak+1+-----+ak+5=0,k∈N*,
所以,S2008=a1+a2+a3+a4=a2+a3=1007
(3)当p=0时,{an}是周期数列,
因为此时an=0(n∈N*)为常数列,
所以对任意给定的正整数T及任意正整数n,
都有an+T=an,符合周期数列的定义.
当p∈(0,
 )时,{an}是递增数列,不是周期数列.
)时,{an}是递增数列,不是周期数列.下面用数学归纳法进行证明:
①当n=1时,因为a1=p,p∈(0,
 )
)所以
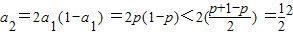 ,
,且a2-a1=2a1(1-a1)-a1=a1(1-2a1)=p(1-2p)>0
所以a1<a2,a2∈(0,
 )
)②假设当n=k时,结论成立,即a1<a2<---<ak,ak∈(0,
 ),
),则ak+1-ak=2ak(1-ak)-ak=ak(1-2ak)>0即ak<ak+1
所以当n=k+1时,结论也成立.
根据①、②可知,{an}是递增数列,不是周期数列.
点评:本题考查了周期函数类比到周期数列,研究周期数列的有关问题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于( )
如图,请观察杨辉三角(杨辉是我国南宋时期的数学家)中各数排列的特征,其中沿箭头所示的数依次组成一个锯齿形数列:1、1、2、3、3、6、4、10、5、…,设此数列的前n项和为Sn,则S2004-2S2005+S2006等于( )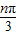 ,n=1,2,3,…
,n=1,2,3,… ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.