题目内容
设数列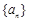 的前n项和为
的前n项和为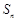 ,点
,点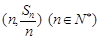 均在直线
均在直线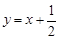 上.
上.
(1)求数列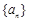 的通项公式;(2)设
的通项公式;(2)设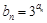 ,试证明数列
,试证明数列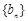 为等比数列.
为等比数列.
【答案】
(1)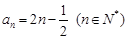 ;(2)只需证
;(2)只需证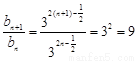 即可。
即可。
【解析】
试题分析:(1)依题意得,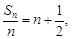 即
即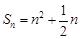 . (2分)
. (2分)
当n≥2时,
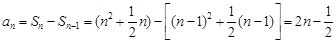 ; (6分)
; (6分)
当n=1时,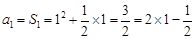 . (7分)
. (7分)
所以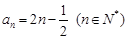 . (8分)
. (8分)
(2)证明:由(1)得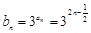 , (9分)
, (9分)
∵ 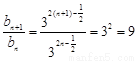 , (11分)
, (11分)
∴  为等比数列. (12分)
为等比数列. (12分)
考点:等差数列的性质;等比数列的性质;数列通项公式的求法。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式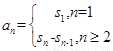 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式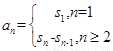 ,用此公式要注意讨论
,用此公式要注意讨论 的情况。
的情况。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,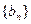 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.