题目内容
设定义在(0,+∞)上的函数f(x)=ax+ +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y= x,求a,b的值.
x,求a,b的值.
【答案】
(1) 2+b (2) a=2,b=-1
【解析】
解:(1)法一 由题知,f(x)=ax+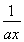 +b≥2+b,
+b≥2+b,
其中当且仅当ax=1时等号成立,
即当x=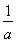 时,f(x)取最小值为2+b.
时,f(x)取最小值为2+b.
法二 f(x)的导数f′(x)=a- =
= ,
,
当x>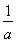 时,f′(x)>0,f(x)在(
时,f′(x)>0,f(x)在(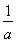 ,+∞)上递增;
,+∞)上递增;
当0<x<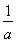 时,f′(x)<0,f(x)在(0,
时,f′(x)<0,f(x)在(0,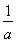 )上递减.
)上递减.
所以当x=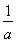 时,f(x)取最小值为2+b.
时,f(x)取最小值为2+b.
(2) f′(x)=a- ,
,
由题设知,f′(1)=a-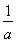 =
= ,
,
解得a=2或a=-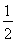 (不合题意,舍去).
(不合题意,舍去).
将a=2代入f(1)=a+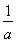 +b=
+b=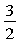 ,解得b=-1.
,解得b=-1.
所以a=2,b=-1.

练习册系列答案
相关题目
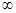 )上的函数
)上的函数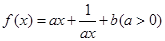
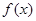 的最小值;
的最小值;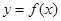 在点
在点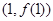 处的切线方程为
处的切线方程为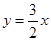 ,求
,求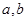 的值.
的值.