题目内容
设定义在[0,2]上的函数![]() 满足下列条件:
满足下列条件:
①对于![]() ,总有
,总有![]() ,且
,且![]() ,
,![]() ;
;
②对于![]() ,若
,若![]() ,则
,则![]() .
.
证明:(1)![]() (
(![]() );(2)
);(2)![]() 时,
时,![]() .
.
证明略
解析:
由![]() 知,函数
知,函数![]() 图像关于直线
图像关于直线![]() 对称,则根据②可知:对于
对称,则根据②可知:对于![]() ,若
,若![]() ,则
,则![]() .……………2分
.……………2分
设![]() ,且
,且![]() ,则
,则![]() .
.
∵![]()
![]() ,
,
∴![]() 在[0,1]上是不减函数.………………………………………………4分
在[0,1]上是不减函数.………………………………………………4分
(1)∵![]() ,
,
∴![]()
![]() .…………………………………………………………8分
.…………………………………………………………8分
(2)对于任意![]() ,则必存在正整数
,则必存在正整数![]() ,使得
,使得![]() .
.
因为![]() 在(0,1)上是不减函数,所以
在(0,1)上是不减函数,所以![]() ,
,
由(1)知![]() .
.
由①可得![]() ,在②中,令
,在②中,令![]() ,得
,得![]() ,∴
,∴![]() .
.
而![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴![]() 时,
时,![]() ..………………………………………12分
..………………………………………12分
∵![]() 时,
时,![]() ,且
,且![]() ,∴
,∴![]() ,
,
因此,![]() 时,
时,![]() .…………………….………….14分
.…………………….………….14分

练习册系列答案
相关题目
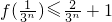 (n∈N*);
(n∈N*);