Question

设数列a₁,a₂,…,a_n,…的前n项和S_n和a_n的关系是S_n=1-ba_n-,其中b是与n无关的常数，且b≠-1.

(1)求a_n和a_n-1的关系式；

(2)写出用n和b表示a_n的表达式；

(3)当0＜b＜1时，求极限S_n.

Answer 1

解：(1)a_n=S_n-S_n-1=-b(a_n-a_n-1)-=-b(a_n-a_n-1)+(n≥2),解得a_n=a_n-1+(n≥2).

(2)∵a₁=S₁=1-ba₁-,∴a₁=.

∴a_n=

….

由此猜想a_n=

把a₁=代入上式得

a_n=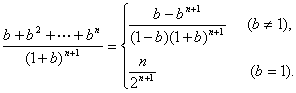

(3)S_n=1-ba_n-=1-b·-=1--

(b≠1).

∵当0＜b＜1时,bⁿ=0,()ⁿ=0,

∴S_n=1.