Question

设数列a₁,a₂,…,a_n,…的前n项和S_n和a_n的关系是S_n=1-ba_n-,其中b是与n无关的常数,且b≠-1.

(1)求a_n与a_n-1的关系式;

(2)写出用n和b表示a_n的表达式;

(3)当0＜b＜1时,求极限S_n.

Answer 1

解析:(1)S_n-1=1-ba_n-1 -,?

S_n-S_n-1=a_n=1-ba_n-1+ba_n-1+,

(b+1)a_n=ba_n-1+,?

a_n=a_n-1+.?

(2)a_n·（b+1)ⁿ=b·（b+1)^n-1a_n-1+.?

①b≠1,令c_n=a_n(b+1)ⁿ, c_n=b·a_n-1+.?

设c_n+λ=b(c_n-1+λ),c_n=bc_n-1+λ(b-1),?

=λ(b-1),λ=.?

∴c_n+bb²-1=b(c_n-1+).?

令d_n=c_n+bb²-1,d_n=d₁·b_n-1 ,c_n+ =d₁·b^n-1 ,?

a_n(b+1)ⁿ=d₁b^n-1-,?

a_n=.?

a₁=1-ba₁-,?

a₁=，C₁=,d₁=.?

∴a_n=?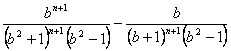

.?

②b=1，则a_n==a_n-1·2^n-1+.?

令x_n=a_n·2ⁿ，x_n=x_n-1?+.?

x₁=2a₁=,x_n=+(n-1)×=.?

a_n= .?

(3)∵b≠1,∴S_n=1+b×.?

∵0＜b＜1,∴b+1＞1.n→∞时,→0.?

S_n=1+.?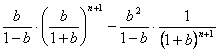

∵1+b＞1,0＜b＜1,?

∴0＜＜1,0＜＜1.?

∴当n→∞时,（)ⁿ⁺¹→0,( )ⁿ⁺¹→0.?

∴→0,→0.?

∴S_n=1.