题目内容
(本小题满分12分)
数列
的前
项和记为
，
.
（1）求的通项公式；
（2）等差数列
的各项为正，其前项和为
且
,又
成
等比数列，求的通项公式；
题
解：（Ⅰ）由
，得
当
时 
，两式相减得
，
所以
-------------------------------------2分
所以
-------------------------------------3分
又
所以
，
从而
---------------------------------5分
而
，不符合上式，
所以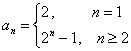
-------------------------------------6分
（Ⅱ）（1）因为
为等差数列，且前三项的和
，所以
，--------7分
可设
由于
，于是
，
因为
成等比数列，
所以
，
或
（舍）
所以
-----------------------------------9分
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
