题目内容
4.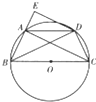 如图,BC是⊙O的直径,AD是平行于BC的弦,过点D作AC的平行线DE,交BA的延长线于点E.
如图,BC是⊙O的直径,AD是平行于BC的弦,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB
(2)DE•DC=AE•BD.
分析 (1)证明∠DBC=∠ACB,即可证明△ABC≌△DCB
(2)证明△AED∽△BAC,可得AE•AC=AB•DE,利用△ABC≌△DCB,可得AB=DC,AC=BD,即可证明DE•DC=AE•BD.
解答 证明:(1)∵AD∥BC,
∴∠ADB=∠DBC,
∵∠ADB=∠ACB,
∴∠DBC=∠ACB
在△ABC和△DCB中,
∵∠BAC=∠DCB,BC=BC,∠DBC=∠ACB,
∴△ABC≌△DCB;
(2)在△AED和△BAC中,
∵AC∥ED,AD∥BC,
∴∠ADE=∠BCA,∠EAD=∠ABC,
∴△AED∽△BAC,
∴$\frac{AE}{AB}=\frac{DE}{AC}$,
∴AE•AC=AB•DE,
∵△ABC≌△DCB,
∴AB=DC,AC=BD,
∴DE•DC=AE•BD.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.设函数f(x)=-x2+2x+3,x∈[-5,5].若从区间内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
9.函数f(x)=x2+ax+2在区间[1,5]上至少有一个零点,则实数a的取值范围为( )
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
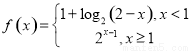 ;
;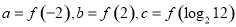 ,则( )
,则( )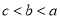 B.
B.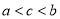
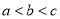 D.
D.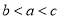
 中,角
中,角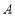 ,
,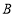 ,
,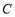 所对的边分别为
所对的边分别为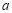 ,
,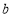 ,
,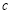 满足
满足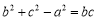 ,
,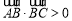 ,
,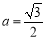 ,则
,则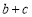 的取值范围是( )
的取值范围是( ) B.
B.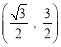
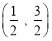 D.
D.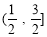
 中,若
中,若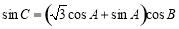 ,则( )
,则( )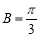

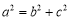 或
或