题目内容
(本小题满分12分)请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.

【答案】
解:设包装盒的高为h(cm),底面边长为a(cm),由已知得

(1)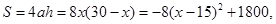
所以当x=15时,S取得最大值.
(2)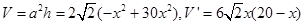 .
.
由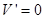 得x=0(舍)或x=20.
得x=0(舍)或x=20.
当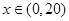 时,
时,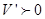 ;当
;当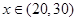 时,
时,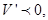
所以当x=20时,V取得极大值,也是最大值.
此时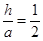 ,即包装盒的高与底面边长的比值为
,即包装盒的高与底面边长的比值为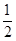 .
.
【解析】略

练习册系列答案
相关题目