题目内容
过点（4，2）作圆（x-1）2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为（ ）
| A．3x+2y+4=0 | B．3x+2y-4=0 | C．3x-2y+4=0 | D．3x-2y-4=0 |
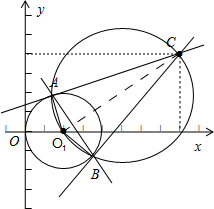
如图：点C（4，2），CB和AC是圆O1：（x-1）2+y2=1的两条切线，
以O1C=
为直径做一个圆，线段O1C的中点坐标为（
，1）
则以O1C为直径的圆的方程为（x-
）2+（y-1）2=
，
由切线性质得O1B⊥CB，
再根据直径O1C对的圆周角等于直角，
则两圆的交点是B、A，两圆的公共弦为AB．
将两圆的方程相减可得公共弦AB的方程3x+2y-4=0，
故答案为：B．
以O1C=
| 13 |
| 5 |
| 2 |
则以O1C为直径的圆的方程为（x-
| 5 |
| 2 |
| 13 |
| 4 |
由切线性质得O1B⊥CB，
再根据直径O1C对的圆周角等于直角，
则两圆的交点是B、A，两圆的公共弦为AB．
将两圆的方程相减可得公共弦AB的方程3x+2y-4=0，
故答案为：B．
练习册系列答案
阅读快车系列答案
相关题目
