题目内容
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.(1)把y表示成θ的函数y=f(θ),并求出定义域;
(2)当m=
| ||||
| 2 |
分析:(1)由题意可得AB=rtanθ,AC=rtan(
-θ),可得y=ar[m2tanθ+tan(
-θ)],由正切函数的定义域可得可得函数的定义域为:(
,
);
(2)由(1)可得y=ar[m2tanθ+tan(
-θ)],可化为y=ar[m2(tanθ-1)+
+m2+1],由基本不等式可得m2(tanθ-1)+
≥2
m,由取等号的条件可得答案.
| 3π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
(2)由(1)可得y=ar[m2tanθ+tan(
| 3π |
| 4 |
| 2 |
| 1-tanθ |
| 2 |
| 1-tanθ |
| 2 |
解答:解:(1)∵BC与圆O相切于A,∴OA⊥BC,在△OAB中,AB=rtanθ,…(2分)
同理,可得AC=rtan(
-θ)…(4分)
∴y=m2aAB+aAC=m2artanθ+artan(
-θ),
∴y=ar[m2tanθ+tan(
-θ)],…(6分)
可得函数的定义域为:(
,
)…(8分)
(2)由(1)可得y=ar[m2tanθ+tan(
-θ)]
=ar[m2tanθ+
]
=ar[m2(tanθ-1)+
+m2+1]
∵θ∈(
,
),∴tanθ-1>0,
∴m2(tanθ-1)+
≥2
m,
当且仅当m2(tanθ-1)=
,即tanθ=
-1时取等号,
又m=
,所以tanθ=
,∴θ=60°
故当θ取60°,即A点在O东偏南60°的方向上,总造价最低. …(16分)
同理,可得AC=rtan(
| 3π |
| 4 |
∴y=m2aAB+aAC=m2artanθ+artan(
| 3π |
| 4 |
∴y=ar[m2tanθ+tan(
| 3π |
| 4 |
可得函数的定义域为:(
| π |
| 4 |
| π |
| 2 |
(2)由(1)可得y=ar[m2tanθ+tan(
| 3π |
| 4 |
=ar[m2tanθ+
| -1-tanθ |
| 1-tanθ |
=ar[m2(tanθ-1)+
| 2 |
| tanθ-1 |
∵θ∈(
| π |
| 4 |
| π |
| 2 |
∴m2(tanθ-1)+
| 2 |
| tanθ-1 |
| 2 |
当且仅当m2(tanθ-1)=
| 2 |
| tanθ-1 |
| ||
| m |
又m=
| ||||
| 2 |
| 3 |
故当θ取60°,即A点在O东偏南60°的方向上,总造价最低. …(16分)
点评:本题考查函数的定义域及其求法,涉及基本不等式的应用,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为圆心、
为圆心、 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心 、西南方向上有一条一级公路
、西南方向上有一条一级公路 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆 .已知通往一级公路的道路
.已知通往一级公路的道路 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是 万元,其中
万元,其中 为常数,设
为常数,设 ,总造价为
,总造价为 万元.
万元.
 的函数
的函数 ,并求出定义域;
,并求出定义域; 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?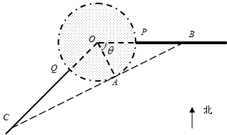 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.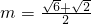 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?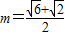 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?