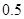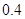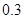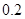题目内容
在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的概率是( )
A.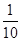 | B.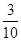 | C.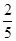 | D.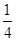 |
C
解析试题分析:取出的2个小球可以是:(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、
(3,4)、(3,5)、(4,5),共10种情况,而取出小球标注的数字之差的绝对值为2或4的有:(1,3)、
(1,5)、(2,4)、(3,5),共4种情况,所以所求概率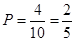 。故选C。
。故选C。
考点:古典概型
点评:求古典概型的概率,通用方法是列举法。

练习册系列答案
相关题目
随机变量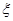 服从二项分布
服从二项分布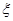 ~
~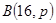 ,且
,且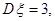 则
则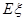 等于( )
等于( )
| A.4 | B.12 | C.4或12 | D.3 |
在区间 上任取2个数
上任取2个数 ,若向量
,若向量 ,则
,则 的概率是
的概率是
A. | B.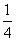 |
C. | D. |
从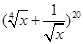 的展开式中任取一项,则取到有理项的概率为( )
的展开式中任取一项,则取到有理项的概率为( )
A.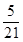 | B.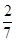 | C.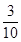 | D.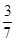 |
已知 , 若
, 若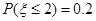 , 则
, 则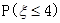 =( )
=( )
| A.0.2 | B.0.3 | C.0.7 | D.0.8 |
若在区域 内任取一点P,则点P恰好在单位圆
内任取一点P,则点P恰好在单位圆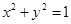 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
已知函数 ,其中
,其中 ,则使得
,则使得 在
在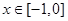 上有解的概率为( )
上有解的概率为( )
A. | B. | C.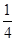 | D. |
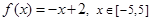 .若从区间
.若从区间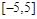 内随机选取一个实数
内随机选取一个实数 ,则所选取的实数
,则所选取的实数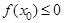 的概率为 ( )
的概率为 ( )