题目内容
设
，则f（2008）的值为 ．
【答案】分析：先利用两个复数代数形式的混合运算化简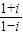
和
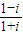，可得f（n）═in+（-i）n，而 i2008=i4×502
=1，可得f（2008）的值．
解答：解：∵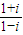
=
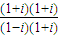=i，
=
=-i．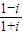
∴
=in+（-i）n，
而 i2008=i4×502=1，∴f（2008）=i2008+（-i）2008=1+1=2，
故答案为：2．
点评：本题主要考查两个复数代数形式的混合运算，虚数单位i的幂运算性质，属于基础题．
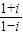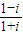和，可得f（n）═in+（-i）n，而 i2008=i4×502 =1，可得f（2008）的值．
解答：解：∵
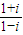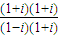==i，==-i．∴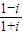
=in+（-i）n，而 i2008=i4×502=1，∴f（2008）=i2008+（-i）2008=1+1=2，
故答案为：2．
点评：本题主要考查两个复数代数形式的混合运算，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
，则f（2008）的值为________．
，则f（2008）的值为 ．