题目内容
(2010•舟山模拟)设f(x)是定义在R上的函数,若f(0)=2008,且对任意x∈R,满足f(x+2)-f(x)≤3•2x,f(x+6)-f(x)≥63•2x,则f(2008)=
.
| ||||
. |
分析:由题设条件,可根据题设中的两个不等式来限定f(2008)的取值范围,从而确定其值,
解答:解:由题意f(2008)≤f(2006)+3×22006≤f(2004)+3×(22006+22004)≤…≤f(0)+3×(22006+22004+…+2 2+2 0)=2008+3×
=2007+22008①
f(2008)≥f(2002)+63•22002,≥f(1996)+63×(22002+21996)≥f(1990)+63(22002+21996+21990)≥…≥f(4)+63(22002+21996+21990+…+24)
=f(4)+63×
=f(4)+22008-24 ②
又已知,又由f(x+2)-f(x)≤3•2 x,f(x+6)-f(x)≥63•2 x可得f(x+6)-f(x+2)≥60•2 x=15•2 x+2,即f(x+4)-f(x)≥15•2 x,
再由f(x+2)-f(x)≤3•2x,得f(x+4)-f(x+2)≤3•2 x+2,两者相加得,得f(x+4)-f(x)≤15•2x,所以f(x+4)-f(x)=15•2x,
∴f(4)-f(0)=15•20=15
∴f(4)=f(0)+15=2008+15=2023,代入②
解得f(2008)≥2007+22008③
由①③得(2008)=2007+22008
故答案为:2007+22008
| 1-41004 |
| 1-4 |
f(2008)≥f(2002)+63•22002,≥f(1996)+63×(22002+21996)≥f(1990)+63(22002+21996+21990)≥…≥f(4)+63(22002+21996+21990+…+24)
=f(4)+63×
| 24×(1-(26)334) |
| 1-64 |
又已知,又由f(x+2)-f(x)≤3•2 x,f(x+6)-f(x)≥63•2 x可得f(x+6)-f(x+2)≥60•2 x=15•2 x+2,即f(x+4)-f(x)≥15•2 x,
再由f(x+2)-f(x)≤3•2x,得f(x+4)-f(x+2)≤3•2 x+2,两者相加得,得f(x+4)-f(x)≤15•2x,所以f(x+4)-f(x)=15•2x,
∴f(4)-f(0)=15•20=15
∴f(4)=f(0)+15=2008+15=2023,代入②
解得f(2008)≥2007+22008③
由①③得(2008)=2007+22008
故答案为:2007+22008
点评:本题考查抽象函数及其应用,解题的关键是根据题设中的两个不等式得出f(2008)的取值范围,根据其范围判断出函数值.本题比较抽象,下手角度很特殊,用到了归纳法的思想,利用归纳推理发现规律在数学解题中经常用到.本题易因为找不到方法而导致出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
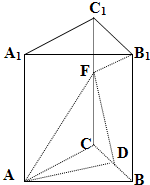 (2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.
(2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.