题目内容
.(本小题满分12分)
已知椭圆的中心在坐标原点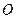 ,焦点在
,焦点在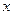 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线 过
过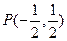 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,
求直线 的方程.
的方程.
已知椭圆的中心在坐标原点
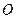 ,焦点在
,焦点在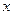 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.(Ⅰ)求椭圆的方程;
(Ⅱ)设直线
 过
过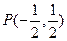 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,求直线
 的方程.
的方程.解:设椭圆方程为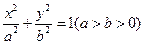 .
.  ……………1分
……………1分
(Ⅰ)由已知可得
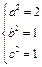 . ……………4分
. ……………4分
∴所求椭圆方程为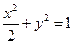 . ……………5分
. ……………5分
(Ⅱ)当直线 的斜率存在时,
的斜率存在时,
设直线 的
的 方程为
方程为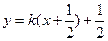 ,
,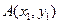
 ,
,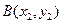
 , ………6分
, ………6分
则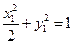 ,
,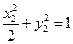 ,两式相减得:
,两式相减得: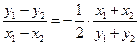 . ………8分
. ………8分
∵P是AB的中点,∴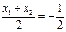 ,
,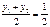 ,
,
代入上式可得直线AB的斜率为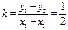 ……10分
……10分
∴直线 的方程为
的方程为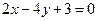 .
.
当直线 的斜率不存在时,将
的斜率不存在时,将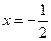 代入椭圆方程并解得
代入椭圆方程并解得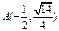 ,
,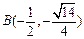 ,
,
这时AB的中点为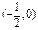 ,
,
∴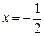 不符合题设要求.综上,直线
不符合题设要求.综上,直线 的方程为
的方程为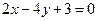 .…12分
.…12分
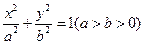 .
.  ……………1分
……………1分(Ⅰ)由已知可得

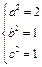 . ……………4分
. ……………4分∴所求椭圆方程为
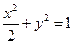 . ……………5分
. ……………5分(Ⅱ)当直线
 的斜率存在时,
的斜率存在时,设直线
 的
的 方程为
方程为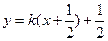 ,
,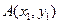
 ,
,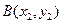
 , ………6分
, ………6分则
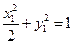 ,
,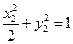 ,两式相减得:
,两式相减得: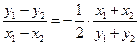 . ………8分
. ………8分∵P是AB的中点,∴
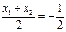 ,
,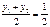 ,
,代入上式可得直线AB的斜率为
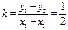 ……10分
……10分∴直线
 的方程为
的方程为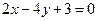 .
.当直线
 的斜率不存在时,将
的斜率不存在时,将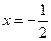 代入椭圆方程并解得
代入椭圆方程并解得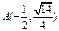 ,
,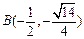 ,
,这时AB的中点为
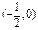 ,
,∴
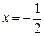 不符合题设要求.综上,直线
不符合题设要求.综上,直线 的方程为
的方程为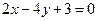 .…12分
.…12分略

练习册系列答案
相关题目
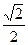 .
.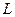 与椭圆交于A、B两点,O为原点,
与椭圆交于A、B两点,O为原点,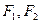 是椭圆
是椭圆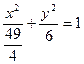 的两个焦点,P是椭圆上的点,若
的两个焦点,P是椭圆上的点,若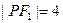 ,则
,则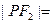 ( )
( ) 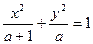
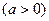 ,倾斜角为
,倾斜角为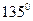 的直线
的直线 过椭圆的左焦点
过椭圆的左焦点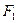 ,与椭圆
,与椭圆 交于
交于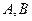 两点,若以
两点,若以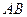 为直径的圆过椭圆的右焦点
为直径的圆过椭圆的右焦点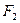 ,求
,求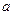 的值.
的值.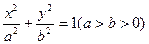 的离心率为
的离心率为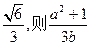 的最小值为
的最小值为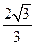
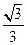
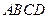 中,
中,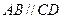 ,且
,且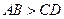 。设以
。设以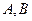 为焦点且过点
为焦点且过点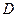 的双曲线的离心率为
的双曲线的离心率为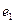 ,以
,以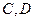 为焦点且过点
为焦点且过点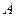 的椭圆的离心率为
的椭圆的离心率为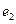 ,则
,则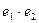 = ;
= ;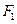 、
、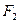 是椭圆
是椭圆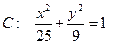 的两个焦点,
的两个焦点,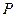 为椭圆上一点,且
为椭圆上一点,且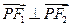 ,若
,若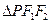 的面积为 .
的面积为 .