题目内容
(本小题满分12分)
如图,在直四棱柱ABCD-A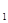 B
B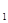 C
C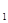 D
D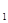 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA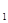 =2,
E、E
=2,
E、E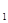 、F分别是棱AD、AA
、F分别是棱AD、AA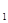 、AB的中点。
、AB的中点。
(1) 证明:直线EE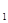 //平面FCC
//平面FCC ;
;
(2) 求二面角B-FC -C的余弦值。
-C的余弦值。
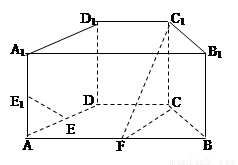
【答案】
(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
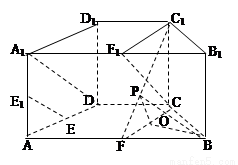
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E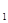 分别是棱AD、AA
分别是棱AD、AA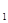 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为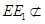 平面FCC
平面FCC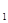 ,
,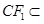 平面FCC
平面FCC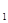 ,
,
所以直线EE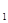 //平面FCC
//平面FCC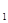 .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A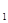 B
B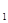 C
C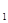 D
D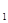 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,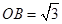 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵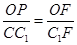 ∴
∴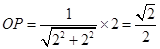 ,
,
在Rt△OPF中,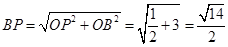 ,
,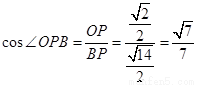 ,所以二面角B-FC
,所以二面角B-FC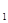 -C的余弦值为
-C的余弦值为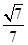 .
.
【解析】略

练习册系列答案
相关题目