题目内容
2.设椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上存在一点P,它与两焦点连线互相垂直,求m的取值范围.分析 根据椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上至少存在一点P,使得它与两焦点连线互相垂直,结合椭圆的性质得:∠F1AF2≥90°,即OA≤$\frac{\sqrt{2}}{2}$AF2,从而得出正实数m的取值范围.
解答 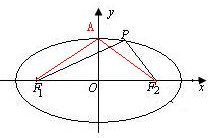 解:如图,∵椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上至少存在一点P,使得它与两焦点连线互相垂直,
解:如图,∵椭圆$\frac{{x}^{2}}{m+25}$+$\frac{{y}^{2}}{m}$=1上至少存在一点P,使得它与两焦点连线互相垂直,
设椭圆的上顶点为A,
结合椭圆的性质得:∠F1AF2≥90°,
∴∠OAF2≥45°,
即OA≤$\frac{\sqrt{2}}{2}$AF2,⇒0<m≤$\frac{1}{2}$(m+25)⇒0<m≤25,
则正实数m的取值范围为(0,25].
故答案为:(0,25].
点评 本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和数形结合能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.某工厂生产的甲、乙、丙三种型号产品的数量之比为2:3:5,现用分层抽样的方法抽取一个容量为n的样本,其中甲种产品有20件,则n=( )
| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
14. 何体的三视图如图所示,则该几何体的表面积是( )
何体的三视图如图所示,则该几何体的表面积是( )
 何体的三视图如图所示,则该几何体的表面积是( )
何体的三视图如图所示,则该几何体的表面积是( )| A. | 8+2$\sqrt{2}$ | B. | 8+4$\sqrt{2}$ | C. | 12+2$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
 从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人
从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,