题目内容
(本小题满分10分)
假定某人每次射击命中目标的概率均为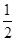 ,现在连续射击3次。
,现在连续射击3次。
(1) 求此人至少命中目标2次的概率;
(2) 若此人前3次射击都没有命中目标,再补射一次后结束射击;否则。射击结束。记此人射击结束时命中目标的次数为X,求X的数学期望。
假定某人每次射击命中目标的概率均为
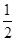 ,现在连续射击3次。
,现在连续射击3次。(1) 求此人至少命中目标2次的概率;
(2) 若此人前3次射击都没有命中目标,再补射一次后结束射击;否则。射击结束。记此人射击结束时命中目标的次数为X,求X的数学期望。
⑴此人至少命中目标2次的概率为 . ⑵
. ⑵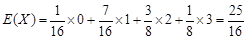 .
.
 . ⑵
. ⑵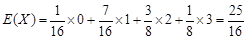 .
. 本试题主要是考查了独立重复试验的事件发生的概率值的求解,以及随机变量的分布列的问题和数学期望值的求解的综合运用。
(1)根据事件的概念,独立事件的乘法公式得到第一问的求解。
(2)然后结合n此独立重复试验的事件发生的概率公式得到各个取值的概率值,进而得到分布列和期望值。
⑴设此人至少命中目标2次的事件为A,则 ,
,
即此人至少命中目标2次的概率为 .…………………………………………… 4分
.…………………………………………… 4分
⑵由题设知 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且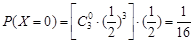 ,
,
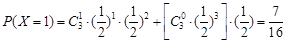 ,
,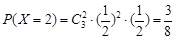 ,
,
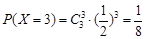 , ………………………………………………………… 8分
, ………………………………………………………… 8分
从而 . ………………………………10分
. ………………………………10分
(1)根据事件的概念,独立事件的乘法公式得到第一问的求解。
(2)然后结合n此独立重复试验的事件发生的概率公式得到各个取值的概率值,进而得到分布列和期望值。
⑴设此人至少命中目标2次的事件为A,则
 ,
, 即此人至少命中目标2次的概率为
 .…………………………………………… 4分
.…………………………………………… 4分⑵由题设知
 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且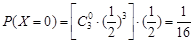 ,
, 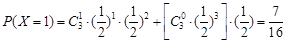 ,
,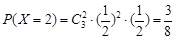 ,
, 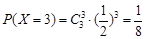 , ………………………………………………………… 8分
, ………………………………………………………… 8分从而
 . ………………………………10分
. ………………………………10分
练习册系列答案
相关题目
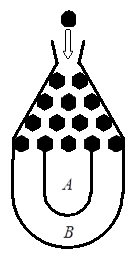
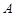 袋或
袋或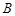 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
.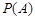 ;
;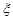 为落入
为落入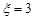 的概率和
的概率和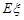 .
.
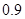 ,播下
,播下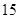 粒种子,恰有
粒种子,恰有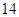 粒发芽的概率为 ( )
粒发芽的概率为 ( )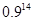
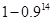
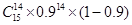
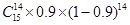
 }为
}为 .如果
.如果 为数列{
为数列{ 项和,那么
项和,那么 的概率为 ( )
的概率为 ( ) 



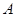 饮料,另外4杯为
饮料,另外4杯为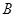 饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯
饮料.公司要求此员工一一品尝后,从8杯饮料中选出4杯 表示此人选对
表示此人选对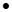 黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)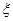 表示所选志愿者中能担任“兼职导游”的人数,试写出
表示所选志愿者中能担任“兼职导游”的人数,试写出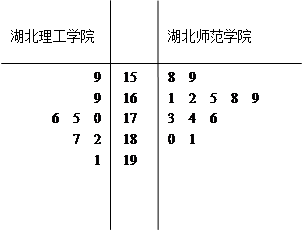
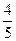 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为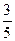 .试求:
.试求: