题目内容
命题“?x∈R,ax2-2ax+3≥0成立”是真命题,则实数a的取值范围为______.
由题意可知,
①当a=0时,原不等式化为“3≥0“对?x∈R显然成立.
②当a≠0时,只需
,即
解得0<a≤3.
综合①②,得0≤a≤3.
故答案为:[0,3].
①当a=0时,原不等式化为“3≥0“对?x∈R显然成立.
②当a≠0时,只需
|
|
解得0<a≤3.
综合①②,得0≤a≤3.
故答案为:[0,3].

练习册系列答案
相关题目
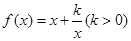 ,
,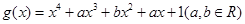 ,(1)若
,(1)若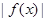 的最小值为2,求
的最小值为2,求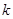 值;(2)设函数
值;(2)设函数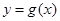 有零点,求
有零点,求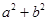 的最小值.
的最小值.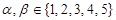 ,那么使得
,那么使得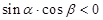 的数对
的数对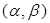 有 个.
有 个.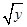
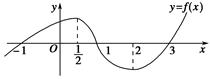
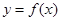 (
(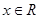 )的图象如图所示,则不等式
)的图象如图所示,则不等式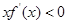 的解集为________.
的解集为________.