Question

（本小题满分12分）

已知关于x的二次函数.

(I)设集合P＝{1,2,3}和Q＝{－1,1,2,3,4}，分别从集合P和Q中随机取一个数作为a和b，求函数在区间上是增函数的概率；

(II)设点(a，b)是区域内的一点，求函数在区间上是增函数的概率．

 

Answer 1

【答案】

(1)所求事件的概率为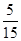＝ ；(2) P＝.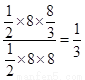

【解析】本题主要考查了古典概型，掌握古典概型的计算步骤和计算公式是解答本题的关键，同时考查了分类的思想，属于基础题．

（1）这是一个古典概型问题，我们分别计算出满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式，即可求解．

（2）根据函数是增函数，得到试验发生包含的事件对应的区域和满足条件的事件对应的区域，做出面积，利用几何概型计算公式得到结果．

(1)∵函数f(x)＝ax²－4bx＋1的图象的对称轴为直线x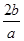＝，要使f(x)＝ax²－4bx＋1在区间[1，＋∞)上为增函数，当且仅当a＞0且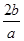≤1，即2b≤a.(2分)

若a＝1，则b＝－1；若a＝2，则b＝－1或1；若a＝3，则b＝－1或1.

∴事件包含基本事件的个数是1＋2＋2＝5.(5分)

∴所求事件的概率为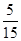＝ (6分)

(2)由(1)，知当且仅当2b≤a且a＞0时，函数f(x)＝ax²－4bx＋1在区间[1，＋∞)上为增函数，(8分)

依条件可知事件的全部结果所构成的区域为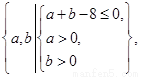，构成所求事件的区域为三角形部分．由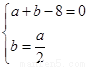得交点坐标为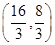，(10分)

∴所求事件的概率为P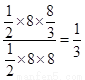＝.(12分)