题目内容
已知长方体ABCD-A1B1C1D1的棱AB=3,AD=2,AA1=2,如图所示,则异面直线AB1与DA1所成的角是 (结果用反三角函数值表示).
【答案】分析:由题意可得,DA1∥CB1,将异面直线AB1与DA1所成的角转化为AB1与CB1所成的角,在△ACB1中,利用余弦定理即可求得答案.
解答:解:∵ABCD-A1B1C1D1的长方体,
∴DA1∥CB1,
∴AB1与DA1所成的角就是AB1与CB1所成的角∠AB1C,
在△ACB1中,AB1=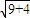 =
=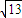 ,CB1=2
,CB1=2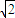 ,AC=
,AC=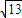 ,
,
∴由余弦定理得,
cos∠AB1C=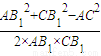
=
=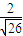
=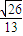 .
.
∴0<∠AB1C<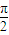
∴∠AB1C=arccos .
.
故答案为:arccos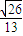 .
.
点评:本题考查异面直线及其所成的角,考查反三角函数的运用,将异面直线AB1与DA1所成的角转化为AB1与CB1所成的角是关键,属于中档题.
解答:解:∵ABCD-A1B1C1D1的长方体,
∴DA1∥CB1,
∴AB1与DA1所成的角就是AB1与CB1所成的角∠AB1C,
在△ACB1中,AB1=
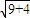 =
=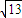 ,CB1=2
,CB1=2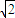 ,AC=
,AC=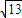 ,
,∴由余弦定理得,
cos∠AB1C=
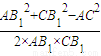
=

=
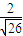
=
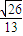 .
.∴0<∠AB1C<
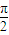
∴∠AB1C=arccos
 .
.故答案为:arccos
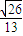 .
.点评:本题考查异面直线及其所成的角,考查反三角函数的运用,将异面直线AB1与DA1所成的角转化为AB1与CB1所成的角是关键,属于中档题.

练习册系列答案
相关题目
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点. 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,
已知长方体ABCD-A1B1C1D1中,DA=DD1=1, 已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2,
已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2, 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.