题目内容
（本小题满分12分）
在数列{an}中，a1=2,a2=8，且已知函数
（
）在x=1时取得极值.(Ⅰ)求证:数列{an+1—2an}是等比数列,（Ⅱ）求数列
的通项an；（Ⅲ）设
，且
对于
恒成立，求实数m的取值范围．
【答案】
解： (Ⅰ) ∵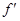
(1)＝0
∴(an＋2－an＋1)－(3a n＋1－4an)＝0
即an＋2－2an＋1＝2(an＋1－2an) 又a2－2a1＝4
∴数列｛an＋1－2an｝是以2为公比，以4为首项的等比数列。...............3分
∴an＋1－2an＝4×2n－1＝2 n＋1
∴
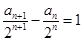且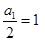
∴数列｛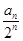
｝是首项为1，公差为1的等差数列，....................5分
∴＝
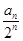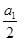＋(n－1)×1＝n
∴
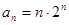.....................................................6分
（Ⅱ）由
，
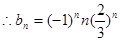
令Sn＝|b1|＋|b2|＋…＋|bn|＝＋2()2＋3()3＋…＋n()n
Sn＝()2＋2()3＋…＋(n－1)()n＋n()n＋1.......................8分
得Sn＝＋()2＋()3＋…＋()n－n()n+1
＝－n()n+1＝2[1－()n]－n()n+1
∴ Sn＝6[1－()n]－3n()n+1＜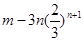
.....................10分
要使得|b1|＋|b2|＋…＋|bn|＜m对于n∈N＊恒成立,只须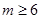
所以实数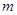
的取值范围是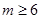。.......................................12分
【解析】略
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
