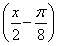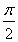在△ABC中.a2+b2+c2＝2absin C.则△ABC的形状是( )A．直角三角形 B．锐角三角形 C．钝角三角形 D．正三角形题目和参考答案——青夏教育精英家教网—

题目内容

在△ABC中，a2＋b2＋c2＝2absin C，则△ABC的形状是(　　)

A．直角三角形 B．锐角三角形 C．钝角三角形 D．正三角形

【解析】a2＋b2＋c2＝a2＋b2＋a2＋b2－2abcos C＝2absin C，即a2＋b2＝2absin，由于2ab≤a2＋b2＝2absin，故只能a＝b且C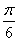＋＝，故三角形为正三角形．也可用特殊值的方法断定正三角形合适，排除其他情况

练习册系列答案

课课练与单元测试系列答案

相关题目

已知等差数列{an}的前n项和为Sn，且S3＝6，则5a1＋a7的值为(　　)

A．12 B．10 C．24 D．6

已知m，n是空间两条不同的直线，α，β，γ是三个不同的平面，则下列命题中为真的是(　　)

A．若α∥β，m?α，n?β，则m∥n

B．若α∩γ＝m，β∩γ＝n，m∥n，则α∥β

C．若m?β，α⊥β，则m⊥α

D．若m⊥β，m∥α，则α⊥β

已知函数f(x)＝＋xln x，则曲线y＝f(x)在x＝1处的切线方程为(　　)

A．x－y－3＝0 B．x－y＋3＝0 C．x＋y－3＝0 D．x＋y＋3＝0

在△ABC中，a，b，c分别为角A，B，C的对边，三边a，b，c成等差数列，且B＝，则|cos A－cos C|的值为________．

tan(－1 410°)的值为(　　)

A. B．－ C. D．－

抽样统计甲、乙两位射击运动员的5次训练成绩(单位：环)，结果如下：

则成绩较为稳定(方差较小)的那位运动员成绩的方差为________．

设a＝(1－3x2)dx＋4，则二项式x2＋6的展开式中不含x3项的系数和是(　　)

A．－160 B．160 C．161 D．－160

已知函数f(x)＝sin(ωx＋φ)(ω>0，|φ|<π)的部分图像如图所示，

(1)求ω，φ的值；

(2)设g(x)＝2f f－1，当x∈[0，]时，求函数g(x)的值域．

试题分类