��Ŀ����
��֪�����д�С��ͬ��1�������3�������Һ����д�С��ͬ��2�������4�������ִӼס����������ڸ���ȡ2����
������ȡ����4������ǡ��1������ĸ��ʣ�
�����衰�Ӽ���ȡ����2����ǡ��1��Ϊ����Ϊ�¼�A�������Һ���ȡ����2�����Ǻ���Ϊ�¼�B�������¼�A�����������£��¼�B�����ĸ��ʣ�
�������Ϊȡ����4�����к���ĸ�������εķֲ��к���ѧ������
������ȡ����4������ǡ��1������ĸ��ʣ�
�����衰�Ӽ���ȡ����2����ǡ��1��Ϊ����Ϊ�¼�A�������Һ���ȡ����2�����Ǻ���Ϊ�¼�B�������¼�A�����������£��¼�B�����ĸ��ʣ�
�������Ϊȡ����4�����к���ĸ�������εķֲ��к���ѧ������
�����������衰�Ӽ���ȡ����2�����Ϊ�����Һ���ȡ����2�����У�1���Ǻ���1���Ǻ���Ϊ�¼�C�����Ӽ���ȡ����2�����У�1���Ǻ���1���Ǻ����Һ���ȡ����2�����Ϊ����Ϊ�¼�D�����¼�C��D���⣬�����ȡ����4������ǡ��1������ĸ��ʣ�
���������P��A��������P��AB��=P��D�����ɴ������������ʹ�ʽP��B/A��=
��������¼�A�����������£��¼�B�����ĸ��ʣ�
����������֪�ο��ܵ�ȡֵΪ0��1��2��3���ֱ����P����=0����P����=1����P����=2����P����=3���ɴ�������εķֲ��е���ѧ������
���������P��A��������P��AB��=P��D�����ɴ������������ʹ�ʽP��B/A��=
| P(AB) |
| P(A) |
����������֪�ο��ܵ�ȡֵΪ0��1��2��3���ֱ����P����=0����P����=1����P����=2����P����=3���ɴ�������εķֲ��е���ѧ������
����⣺�����衰�Ӽ���ȡ����2�����Ϊ�����Һ���ȡ����2�����У�1���Ǻ���1���Ǻ���Ϊ�¼�C�����Ӽ���ȡ����2�����У�1���Ǻ���1���Ǻ����Һ���ȡ����2�����Ϊ����Ϊ�¼�D�������¼�C��D���⣬
��P��C��=
•
=
��
P��D��=
•
=
��
��ȡ����4������ǡ��1������ĸ���Ϊ
P��C+D��=P��C��+P��D��=
+
=
��
���ߡ��Ӽ���ȡ����2����ǡ��1��Ϊ����Ϊ�¼�A��
��P��A��=
=
��
�ߡ����Һ���ȡ����2�����Ǻ���Ϊ�¼�B��
��P��AB��=P��D��=
��
�����¼�A�����������£��¼�B�����ĸ���P��B/A��=
=
=
��
����������֪�ο��ܵ�ȡֵΪ0��1��2��3��
�ɣ�������P����=0��=
•
=
��
P����=1��=
��
P����=3��=
•
=
��
��P����=2��=1-P����=0��-P����=1��-P����=3��=
��
��εķֲ���Ϊ
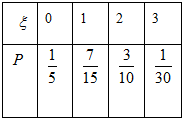
��ε���ѧ����E��=0��
+1��
+2��
+3��
=
������12�֣�
��P��C��=
| ||
|
| ||||
|
| 4 |
| 15 |
P��D��=
| ||
|
| ||
|
| 1 |
| 5 |
��ȡ����4������ǡ��1������ĸ���Ϊ
P��C+D��=P��C��+P��D��=
| 4 |
| 15 |
| 1 |
| 5 |
| 7 |
| 15 |
���ߡ��Ӽ���ȡ����2����ǡ��1��Ϊ����Ϊ�¼�A��
��P��A��=
| ||||
|
| 1 |
| 2 |
�ߡ����Һ���ȡ����2�����Ǻ���Ϊ�¼�B��
��P��AB��=P��D��=
| 1 |
| 5 |
�����¼�A�����������£��¼�B�����ĸ���P��B/A��=
| P(AB) |
| P(A) |
| ||
|
| 2 |
| 5 |
����������֪�ο��ܵ�ȡֵΪ0��1��2��3��
�ɣ�������P����=0��=
| ||
|
| ||
|
| 1 |
| 5 |
P����=1��=
| 7 |
| 15 |
P����=3��=
| ||
|
| 1 | ||
|
| 1 |
| 30 |
��P����=2��=1-P����=0��-P����=1��-P����=3��=
| 3 |
| 10 |
��εķֲ���Ϊ

��ε���ѧ����E��=0��
| 1 |
| 5 |
| 7 |
| 15 |
| 3 |
| 10 |
| 1 |
| 30 |
| 7 |
| 6 |
���������⿼����ɢ����������ķֲ�������ѧ�������������������ʵ�������ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ