题目内容
(本小题满分12分)已知函数
(I)求 的单调区间;
的单调区间;
(II)若对于任意的 ,都有
,都有 求a的取值范围。
求a的取值范围。
解:
(Ⅰ)f¢(x)=2(x-a)ex+(x-a)2ex=(x-a)[x-(a-2)]ex.…………………………2分
令f¢(x)=0,得x1=a-2,x2=a.
当x变化时,f¢ (x)、f(x)的变化如下:
(x)、f(x)的变化如下:
所以
f(x)的单调递增区间是(-∞,a-2),(a,+∞),
单调递减区间是(a-2,a).………………………………………………………7分
(Ⅱ)当x∈(-∞,1]时,
由(Ⅰ)知,f(x)在(-∞,a-2)单调递增,在(a-2,a)单调递减,在(a,1)单调递增,f(x)在(-∞,1]上的最大值为f(a-2)或f(1).
当a∈[-1,3],f(a-2)=4ea-2≤4e;f(1)=(a-1)2e≤4e,
所以f(x)≤4e.……………………………………………………………………12分
解析

练习册系列答案
相关题目
设 是将函数
是将函数 向左平移
向左平移 个单位得到的,则
个单位得到的,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
若 是定义在R上的连续函数,且
是定义在R上的连续函数,且 ,则
,则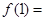 ( )
( )
| A.2 | B.1 | C.0 | D.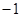 |
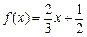 ,
,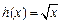 .
.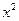 [h(x)]
[h(x)]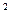 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;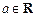 ,解关于x的方程
,解关于x的方程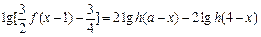 ;
;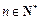 ,证明:
,证明: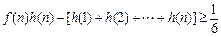 .
.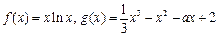 .
.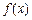 的单调区间;
的单调区间;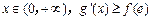 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.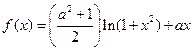

 .
.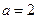 时,求
时,求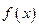 的极值
的极值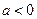 时,讨论
时,讨论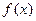 的单调性。
的单调性。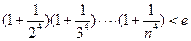 (
(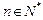 ,
,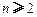 ,其中无理数
,其中无理数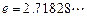 )
)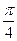 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由. 分13分)已知
分13分)已知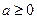 ,函数
,函数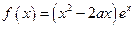 .
.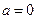 时讨论函数的单调性;
时讨论函数的单调性;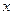 取何值时,
取何值时,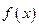 取最小值,证明你的结论.
取最小值,证明你的结论. 的图象过点(1, -4),且函数
的图象过点(1, -4),且函数 的图象关于y轴对称.
的图象关于y轴对称. 的极值;
的极值; 在区间
在区间 上的最大值。
上的最大值。