题目内容
双曲线 (a,b>0),一焦点到其相应准线的距离为
(a,b>0),一焦点到其相应准线的距离为 ,过点A(0,-b),B(a,0)的直线与原点的距离为
,过点A(0,-b),B(a,0)的直线与原点的距离为 ,
,
(1)求该双曲线的方程;
(2)是否存在直线y=kx+5 (k≠0)与双曲线交于相异两点C,D,使得 C,D两点都在以A为圆心的同一个圆上,若存在,求出直线方程;若不存在说明理由.
解:(1)因为焦点到其相应准线的距离为 ,所以
,所以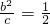 ;
;
又因为过点A(0,-b),B(a,0)的直线与原点的距离为 ;
;
可设直线方程为 ,
,
由点到直线的距离公式得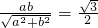 ,解得a=
,解得a= ,b=1,
,b=1,
所以双曲线方程为
(2)假设存在直线y=kx+5(k≠0,)与双曲线交于相异两点C,D,使得C,D两点都在以A为圆心的同一个圆上
∴ 得(1-3k2)x2-30kx-78=0;可得
得(1-3k2)x2-30kx-78=0;可得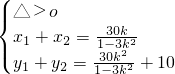
因为C,D两点都在以A为圆心的同一个圆上;所以有|AC|=|AD|,
所以直线CD的中点坐标为M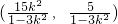
因为AM⊥CD,所以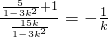 ,解得k=
,解得k= ,
,
所以直线方程为:y= x+5
x+5
分析:(1)根据焦点到其相应准线的距离求得b和c的关系,设出直线AB的方程,进而利用点到直线的距离公式求得a和b,则双曲线的方程可得.
(2)假设直线存在,把直线与双曲线方程联立消去y,根据韦达定理表示出x1+x2和y1+y2,根据C,D两点都在以A为圆心的同一个圆上推断出|AC|=|AD|,进而求得CD中点的表达式,根据AM⊥CD,分别表示出其斜率,乘积为-1求得k,则直线方程可得.
点评:本题主要考查了双曲线的标准方程和直线与双曲线的关系.考查了学生综合分析问题和解决问题的能力.运算能力的考查.
 ,所以
,所以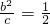 ;
;又因为过点A(0,-b),B(a,0)的直线与原点的距离为
 ;
;可设直线方程为
 ,
,由点到直线的距离公式得
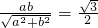 ,解得a=
,解得a= ,b=1,
,b=1,所以双曲线方程为

(2)假设存在直线y=kx+5(k≠0,)与双曲线交于相异两点C,D,使得C,D两点都在以A为圆心的同一个圆上
∴
 得(1-3k2)x2-30kx-78=0;可得
得(1-3k2)x2-30kx-78=0;可得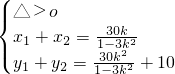
因为C,D两点都在以A为圆心的同一个圆上;所以有|AC|=|AD|,
所以直线CD的中点坐标为M
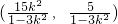
因为AM⊥CD,所以
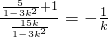 ,解得k=
,解得k= ,
,所以直线方程为:y=
 x+5
x+5分析:(1)根据焦点到其相应准线的距离求得b和c的关系,设出直线AB的方程,进而利用点到直线的距离公式求得a和b,则双曲线的方程可得.
(2)假设直线存在,把直线与双曲线方程联立消去y,根据韦达定理表示出x1+x2和y1+y2,根据C,D两点都在以A为圆心的同一个圆上推断出|AC|=|AD|,进而求得CD中点的表达式,根据AM⊥CD,分别表示出其斜率,乘积为-1求得k,则直线方程可得.
点评:本题主要考查了双曲线的标准方程和直线与双曲线的关系.考查了学生综合分析问题和解决问题的能力.运算能力的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目