题目内容
已知数列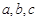 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d 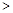 0).在
0).在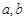 之间和b,c之间共插入
之间和b,c之间共插入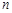 个实数,使得这
个实数,使得这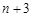 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证: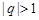 ;
;
(2)若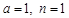 ,求
,求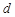 的值;
的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且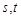 都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用 表示).
表示).
【答案】
解:(1)由题意知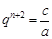 ,
, ,
,
又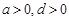 ,可得
,可得 ,
………………………………2分
,
………………………………2分
即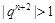 ,故
,故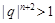 ,又
,又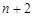 是正数,故
是正数,故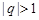 .………………………………4分
.………………………………4分
(2)由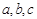 是首项为1、公差为
是首项为1、公差为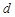 的等差数列,故
的等差数列,故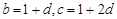 ,
,
若插入的这一个数位于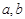 之间,则
之间,则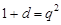 ,
,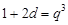 ,
,
消去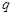 可得
可得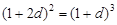 ,即
,即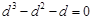 ,其正根为
,其正根为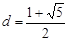 .………7分
.………7分
若插入的这一个数位于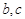 之间,则
之间,则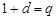 ,
,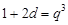 ,
,
消去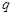 可得
可得 ,即
,即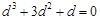 ,此方程无正根.
,此方程无正根.
故所求公差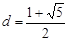 . ………………………………………9分
. ………………………………………9分
(3)由题意得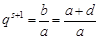 ,
,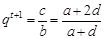 ,又
,又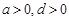 ,
,
故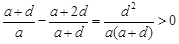 ,可得
,可得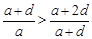 ,又
,又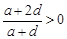 ,
,
故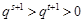 ,即
,即 .
.
又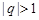 ,故有
,故有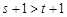 ,即
,即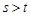 .
………………………………………12分
.
………………………………………12分
设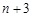 个数所构成的等比数列为
个数所构成的等比数列为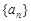 ,则
,则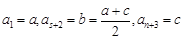 ,
,
由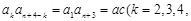 …,
…,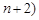 ,可得
,可得
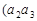 …
…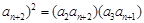 …
…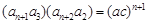 ,
……………………14分
,
……………………14分
又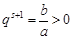 ,
,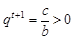 ,
,
由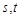 都为奇数,则q既可为正数,也可为负数,
都为奇数,则q既可为正数,也可为负数,
①若q为正数,则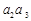 …
…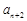
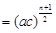 ,插入n个数的乘积为
,插入n个数的乘积为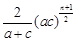 ;
;
②若q为负数,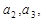 …
…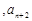 中共有
中共有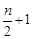 个负数,
个负数,
故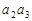 …
…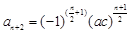 ,所插入的数的乘积为
,所插入的数的乘积为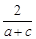
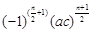 .
.
所以当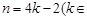 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为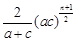 ;
;
当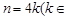 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为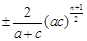 . …………………18分
. …………………18分
(另法:由又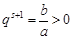 ,
,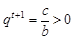 ,
,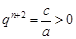
由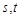 都为奇数,可知
都为奇数,可知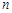 是偶数,q既可为正数也可为负数.
是偶数,q既可为正数也可为负数.
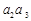 …
…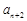
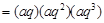 …
…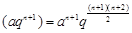
①若q为正数,则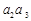 …
…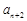
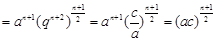 ,
,
故插入n个数的乘积为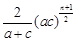 ;
…………………15分
;
…………………15分
②若q为负数,由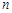 是偶数,可知
是偶数,可知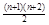 的奇偶性与
的奇偶性与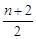 的奇偶性相同,
的奇偶性相同,
可得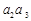 …
…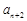
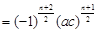 .
.
所以当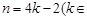 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为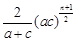 ;
;
当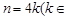 N*)时,所插入n个数的积为
N*)时,所插入n个数的积为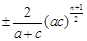 . …………………18分)
. …………………18分)
【解析】略

练习册系列答案
相关题目
 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意的
项和,对于任意的 ,满足关系式
,满足关系式
 的通项公式是
的通项公式是 ,前
,前 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有
 的各项均为正实数,且其前
的各项均为正实数,且其前 项和
项和 满足
满足 。(1)证明:数列
。(1)证明:数列 ,求数列
,求数列 的前
的前 。
。 是各项均为正整数的等差数列,公差
是各项均为正整数的等差数列,公差 ,且
,且 ,则
,则 的取值集合为
;
的取值集合为
; ,则
,则