题目内容
已知数列{an}是各项均为正整数的等差数列,公差d∈N*,且{an}中任意两项之和也是该数列中的一项.(1)若a1=4,则d的取值集合为
(2)若a1=2m(m∈N*),则d的所有可能取值的和为
分析:由题意可得,ap+aq=ak,其中p、q、k∈N*,利用等差数列的通项公式可得d与a1的关系,然后根据d的取值范围进行求解.
解答:解:由题意可得,ap+aq=ak,其中p、q、k∈N*,
由等差数列的通向公式可得a1+(p-1)d+a1+(q-1)d=a1+(k-1),
整理得d=
,
(1)若a1=4,则d=
,
∵p、q、k∈N*,公差d∈N*,
∴k-p-q+1∈N*,
∴d=1,2,4,
故d的取值集合为 {1,2,4};
(2)若a1=2m(m∈N*),则d=
,
∵p、q、k∈N*,公差d∈N*,
∴k-p-q+1∈N*,
∴d=1,2,4,…,2m,
∴d的所有可能取值的和为1+2+4+…+2m=
=2m+1-1,
故答案为(1){1,2,4},(2)2m+1-1.
由等差数列的通向公式可得a1+(p-1)d+a1+(q-1)d=a1+(k-1),
整理得d=
| a1 |
| k-p-q+1 |
(1)若a1=4,则d=
| 4 |
| k-p-q+1 |
∵p、q、k∈N*,公差d∈N*,
∴k-p-q+1∈N*,
∴d=1,2,4,
故d的取值集合为 {1,2,4};
(2)若a1=2m(m∈N*),则d=
| 2m |
| k-p-q+1 |
∵p、q、k∈N*,公差d∈N*,
∴k-p-q+1∈N*,
∴d=1,2,4,…,2m,
∴d的所有可能取值的和为1+2+4+…+2m=
| 1×(1-2m+1) |
| 1-2 |
故答案为(1){1,2,4},(2)2m+1-1.
点评:本题考查了等差数列的通项公式,运用了解方程求正整数根的解题思想,特别注意p、q、k、d∈N*这一条件的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
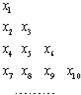 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足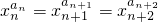 (n∈N*).
(n∈N*).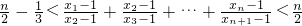 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.