题目内容
2、已知数列{an}是各项均为正整数的等比数列，数列{bn}是等差数列，且a6=b7，则有（ ）
分析：先根据等比数列、等差数列的通项公式表示出a6、b7，然后表示出a3+a9和b4+b10，然后二者作差比较即可．
解答：解：∵an=a1qn-1，bn=b1+（n-1）d，
∵a6=b7∴a1q5=b1+6d
a3+a9=a1q2+a1q8
b4+b10=2（b1+6d）=2b7=2a6
a3+a9-2a6=a1q2+a1q8-2a1q5=a1q8-a1q5-（a1q5-a1q2）=a1q2（q3-1）2≥0
所以a3+a9≥b4+b10
故选B．
∵a6=b7∴a1q5=b1+6d
a3+a9=a1q2+a1q8
b4+b10=2（b1+6d）=2b7=2a6
a3+a9-2a6=a1q2+a1q8-2a1q5=a1q8-a1q5-（a1q5-a1q2）=a1q2（q3-1）2≥0
所以a3+a9≥b4+b10
故选B．
点评：本题主要考查了等比数列的性质．比较两数大小一般采取做差的方法．属基础题．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
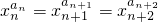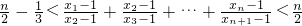（n∈N*）．
．
（n∈N*）．
．
（n∈N*）．
．