题目内容
若过点(0,-1)的直线l与抛物线y2=2x有且只有一个交点,则这样的直线有条.
- A.1
- B.2
- C.3
- D.4
C
分析:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意;当直线的斜率k存在时,当k=0时,可得过点(0,-1)的直线l与抛物线的对称轴平行,与抛物线y2=2x有且只有一个交点,满足条件;当k≠0时,过点(0,-1)的直线l与抛物线y2=2x相切,此时有且只有一个交点,综上可得满足条件的直线条数即可.
解答: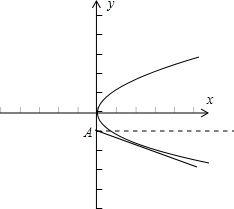 解:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意
解:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意
当直线的斜率k存在时,当k=0时,可得过点(0,-1)的直线l与抛物线的对称轴平行,
与抛物线y2=2x有且只有一个交点,满足条件
当k≠0时,过点(0,-1)的直线l与抛物线y2=2x相切,此时有且只有一个交点,
综上可得满足条件的直线有三条
故选C.
点评:本题主要考查了直线与抛物线的位置关系的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.
分析:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意;当直线的斜率k存在时,当k=0时,可得过点(0,-1)的直线l与抛物线的对称轴平行,与抛物线y2=2x有且只有一个交点,满足条件;当k≠0时,过点(0,-1)的直线l与抛物线y2=2x相切,此时有且只有一个交点,综上可得满足条件的直线条数即可.
解答:
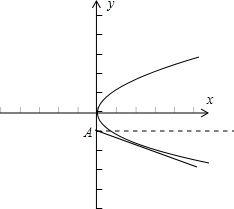 解:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意
解:当直线的斜率不存在时,直线的方程为x=0,与抛物线只有一个交点,满足题意当直线的斜率k存在时,当k=0时,可得过点(0,-1)的直线l与抛物线的对称轴平行,
与抛物线y2=2x有且只有一个交点,满足条件
当k≠0时,过点(0,-1)的直线l与抛物线y2=2x相切,此时有且只有一个交点,
综上可得满足条件的直线有三条
故选C.
点评:本题主要考查了直线与抛物线的位置关系的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目