题目内容
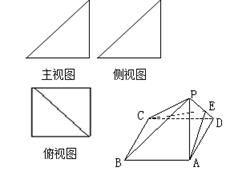
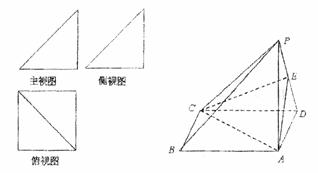
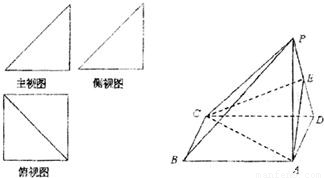
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
(1)求证:PB∥平面ACE;
(2)求证:PC⊥BD;
(3)求三棱锥C-PAB的体积.
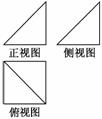
解:(1)证明:依题意,该三视图所对应的几何体为侧棱PA垂直于底面ABCD的四棱锥,且PA=AB=AD=1,四边形ABCD为正方形.

![]() 分别连接AC、BD交于点O,连接EO,
分别连接AC、BD交于点O,连接EO,
∵E是PD的中点,∴PB∥EO.
又PB⊄平面ACE,EO⊂平面ACE,
∴PB∥平面ACE.
(2)证明:∵四边形ABCD是正方形,
∴BD⊥AC.又PA⊥平面ABCD,
∴BD⊥PA.
又∵PA∩AC=A,∴BD⊥平面PAC.
![]() 又PC⊂平面PAC,
又PC⊂平面PAC,
∴PC⊥BD.
(3)∵PA⊥平面ABCD,PA=AB=BC=1,
∴VC-PAB=VP-ABC=![]() ×S△ABC×PA
×S△ABC×PA
=![]() ×
×![]() ×1×1×1=
×1×1×1=![]() .
.
∴三棱锥C-PAB的体积为![]() .
.

练习册系列答案
相关题目
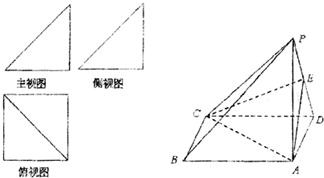 一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.