Question

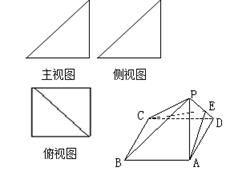
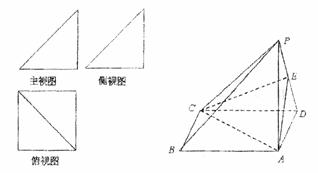
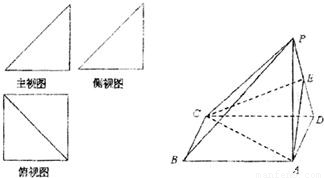
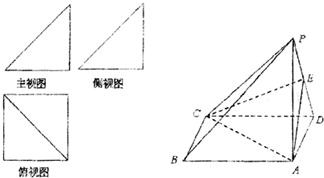一个简单多面体的直观图和三视图如图所示，它的主视图和侧视图都是腰长为1的等腰直角三角形，俯视图为正方形，E是PD的中点．
（Ⅰ）求证：PB∥平面ACE；
（Ⅱ）求证：PC⊥BD；
（Ⅲ）求三棱锥C-PAB的体积．

Answer 1

分析：（I）连接BD，BD∩AC=O，连接OE，根据三角形中位线定理，可得BP∥OE，根据线面平行的判定定理，我们即可得到PB∥平面ACE；
（Ⅱ）由已知俯视图为正方形，主视图和侧视图都是腰长为1的等腰直角三角形，我们易得到AC⊥BD，PA⊥BD，根据线面垂直的判定定理可得BD⊥平面PAC，再由线面垂直的性质，即可得到PC⊥BD；
（Ⅲ）由已知中主视图和侧视图都是腰长为1的等腰直角三角形，俯视图为正方形，我们易得底面为边长为1的正方形，高为1，代入棱锥体积公式，即可得到答案．

解答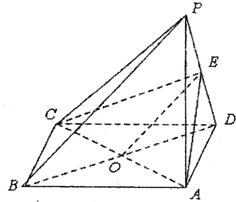：证明：（I）连接BD，BD∩AC=O，连接OE，
易知OE是△BPD的中位线，
∴BP∥OE，
OE?平面ACE，
∴PB∥平面ACE．
（II）∵俯视图为正方形，
即ABCD是正方形，
∴AC⊥BD，
∵PA⊥平面ABCD，
∴PA⊥BD，
PA∩AC=A，BD⊥平面PAC．
PC?平面PAC．
∴PC⊥BD
解：（III）由已知正方形ABCD的边长为1，
PA=1，
V_C-PAB=V_P-ABC=

1

3

•

1

2

•1•1•1=

1

6

．

点评：本题考查的知识点是棱锥的体积，线面平行的判定，及线面垂直的判定和性质，其中（1）的关键是找到BP∥OE，（2）的关键是证出BD⊥平面PAC，（3）的关键是判断几何的棱长及几何体的形状．