Question

已知f（x）是定义在R上的偶函数，且对于任意的x∈R都有f（x+2）=-f（x），若当x∈[0，2]时，f（x）=lg（x+1），则有（　　）

• A．f(1)＞f(-

  3

  2

  )＞f(

  7

  2

  )
• B．f(-

  3

  2

  )＞f(

  7

  2

  )＞f(1)
• C．f(-

  3

  2

  )＞f(1)＞f(

  7

  2

  )
• D．f(

  7

  2

  )＞f(1)＞f(-

  3

  2

  )

Answer 1

分析：由题意求得f（x）是周期等于4的周期函数，画出函数f（x）在一个周期[-2，2]上的图象，根据f（-

3

2

）=f（

3

2

），f（

7

2

）=f（

1

2

），利用函数的单调性求得f(-

3

2

)＞f(1)＞f(

7

2

)

解答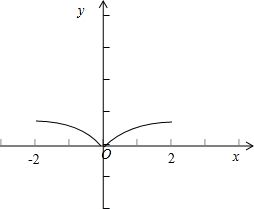：解：函数f（x）对于任意的x∈R都有f（x+2）=-f（x），∴f（x+4）=f（x），故f（x）是周期等于4的周期函数．
∵f（x）是定义在R上的偶函数，x∈[0，2]时，f（x）=lg（x+1），故函数f（x）在一个周期[-2，2]上的图象如图所示：
∴f（x）[-2，0]上是减函数，在[0，2]上是增函数．
再由f（-

3

2

）=f（

3

2

），f（

7

2

）=f（-

7

2

）=f（-

7

2

+4）=f（

1

2

），

1

2

＜1＜

3

2

，∴f（

1

2

）＜f（1）＜f（

3

2

），
∴f(-

3

2

)＞f(1)＞f(

7

2

)，
故选C．

点评：本题主要考查对数函数的单调性和特殊点，体现了化归与转化以及数形结合的数学思想，属于中档题．