题目内容
已知y轴右侧一动圆![]() 与一定圆
与一定圆![]() 外切,也与y轴相切.
外切,也与y轴相切.
(1)求动圆![]() 圆心的轨迹C;
圆心的轨迹C;
(2)过点T(-2,0)作直线l与轨迹C交于A、B两点,求一点![]() ,使得
,使得![]() 是以点E为直角顶点的等腰直角三角形。
是以点E为直角顶点的等腰直角三角形。
(1)动点C1的轨迹C是以(0,0)为顶点,以(2,0)为焦点的抛物线,除去原点.
(2)E点坐标为(10,0)
解析:
(1)由题意知动点C1到定点(2,0)与到定直线![]() 的距离相等,则动点M的轨迹是以定点(2,0)为焦点,定直线
的距离相等,则动点M的轨迹是以定点(2,0)为焦点,定直线![]() 为准线的抛物线。所以点M的轨迹方程为
为准线的抛物线。所以点M的轨迹方程为![]()
又点C1在原点时,动圆不存在,所以,动点C1的轨迹C是以(0,0)为顶点,以
(2,0)为焦点的抛物线,除去原点.
(2)设直线![]() ……①
……①
![]()
设![]() ①的两个实数根,由韦达定理得
①的两个实数根,由韦达定理得
![]() ,
,![]()
所以,线段AB的中点坐标为![]()
而![]()
若x轴上存在一点![]() , 使△AEB是以点E为直角顶点的等腰直角三角形,
, 使△AEB是以点E为直角顶点的等腰直角三角形,
则![]() ,且
,且![]() ,直线EF的方程为:
,直线EF的方程为:![]()
令![]() 得E点坐标为
得E点坐标为![]() ,则
,则![]()
=![]() , 所以
, 所以 ![]() 解得
解得![]() ,
,
则E点坐标为(10,0)

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
 (2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且
(2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且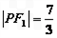 ,求曲线E的标准方程;
,求曲线E的标准方程;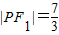 ,求曲线E的标准方程;
,求曲线E的标准方程;