题目内容
已知F1(-1,0)、F2(1,0),圆F2:(x-1)2+y2=1,一动圆在y轴右侧与y轴相切,同时与圆F2相外切,此动圆的圆心轨迹为曲线C,曲线E是以F1,F2为焦点的椭圆.(1)求曲线C的方程;
(2)设曲线C与曲线E相交于第一象限点P,且
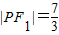 ,求曲线E的标准方程;
,求曲线E的标准方程;(3)在(1)、(2)的条件下,直线l与椭圆E相交于A,B两点,若AB的中点M在曲线C上,求直线l的斜率k的取值范围.
【答案】分析:(1)设动圆圆心的坐标为(x,y)(x>0),由动圆在y轴右侧与y轴相切,同时与圆F2相外切,知|CF2|-x=1,由此能求出曲线C的方程.
(2)依题意,c=1,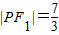 ,得
,得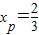 ,由此能求出曲线E的标准方程.
,由此能求出曲线E的标准方程.
(3)设直线l与椭圆E交点A(x1,y1),B(x2,y2),A,B的中点M的坐标为(x,y),将A,B的坐标代入椭圆方程中,得3(x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,由此能够求出直线l的斜率k的取值范围.
解答:解:(1)设动圆圆心的坐标为(x,y)(x>0)
因为动圆在y轴右侧与y轴相切,同时与圆F2相外切,
所以|CF2|-x=1,…(1分)
∴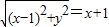 ,
,
化简整理得y2=4x,曲线C的方程为y2=4x(x>0); …(3分)
(2)依题意,c=1,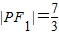 ,
,
得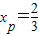 ,…(4分)
,…(4分)
∴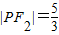 ,
,
又由椭圆定义得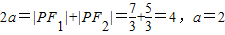 .…(5分)
.…(5分)
∴b2=a2-c2=3,所以曲线E的标准方程为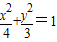 .…(6分)
.…(6分)
(3)设直线l与椭圆E交点A(x1,y1),B(x2,y2),
A,B的中点M的坐标为(x,y),
将A,B的坐标代入椭圆方程中,
得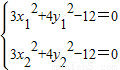 ,
,
两式相减得3(x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,
∴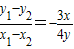 ,…(7分)
,…(7分)
∵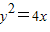 ,
,
∴直线AB的斜率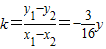 ,…(8分)
,…(8分)
由(2)知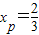 ,
,
∴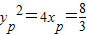 ,∴
,∴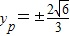
由题设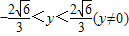 ,
,
∴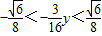 ,…(10分)
,…(10分)
即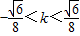 (k≠0).…(12分)
(k≠0).…(12分)
点评:本题考查曲线方程的求法,考查直线的斜率的取值范围的求法,解题时要认真审题,注意点差法和等价转化思想的合理运用.
(2)依题意,c=1,
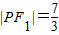 ,得
,得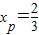 ,由此能求出曲线E的标准方程.
,由此能求出曲线E的标准方程.(3)设直线l与椭圆E交点A(x1,y1),B(x2,y2),A,B的中点M的坐标为(x,y),将A,B的坐标代入椭圆方程中,得3(x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,由此能够求出直线l的斜率k的取值范围.
解答:解:(1)设动圆圆心的坐标为(x,y)(x>0)
因为动圆在y轴右侧与y轴相切,同时与圆F2相外切,
所以|CF2|-x=1,…(1分)
∴
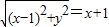 ,
,化简整理得y2=4x,曲线C的方程为y2=4x(x>0); …(3分)
(2)依题意,c=1,
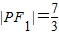 ,
,得
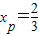 ,…(4分)
,…(4分)∴
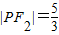 ,
,又由椭圆定义得
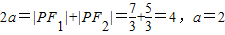 .…(5分)
.…(5分)∴b2=a2-c2=3,所以曲线E的标准方程为
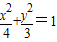 .…(6分)
.…(6分)(3)设直线l与椭圆E交点A(x1,y1),B(x2,y2),
A,B的中点M的坐标为(x,y),
将A,B的坐标代入椭圆方程中,
得
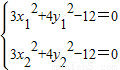 ,
,两式相减得3(x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,
∴
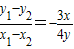 ,…(7分)
,…(7分)∵
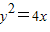 ,
,∴直线AB的斜率
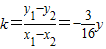 ,…(8分)
,…(8分)由(2)知
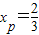 ,
,∴
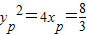 ,∴
,∴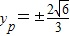
由题设
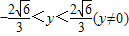 ,
,∴
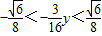 ,…(10分)
,…(10分)即
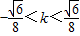 (k≠0).…(12分)
(k≠0).…(12分)点评:本题考查曲线方程的求法,考查直线的斜率的取值范围的求法,解题时要认真审题,注意点差法和等价转化思想的合理运用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目