题目内容
设函数 的最高点D的坐标为(
的最高点D的坐标为( ,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为(
,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为( ,0)。
,0)。
(1)求函数 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值;
的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值;
(3)将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间。
的单调减区间。
 的最高点D的坐标为(
的最高点D的坐标为( ,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为(
,2),由最高点D运动到相邻最低点时,函数图象与x的交点的坐标为( ,0)。
,0)。(1)求函数
 的解析式;
的解析式; (2)当
 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值;
的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值;(3)将函数
 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间。
的单调减区间。 解:(1)∵由最高点D(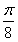 ,2)运动到相邻最低点时,函数图形与的交点的坐标为(
,2)运动到相邻最低点时,函数图形与的交点的坐标为(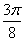 ,0),
,0),
∴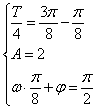 ,
,
从而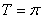 ,
,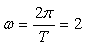 ,
,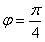 ,
,
∴函数的解析式为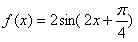 。
。
(2)由(1)得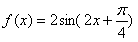 ,
,
当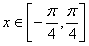 时,
时,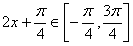 ,
,
∴当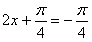 即
即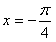 时,函数y取得最小值
时,函数y取得最小值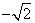 ,
,
当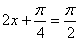 即
即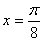 时,函数y取得最大值2。
时,函数y取得最大值2。
(3)由题意,得 ,即
,即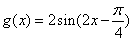 ,
,
由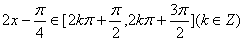 ,得
,得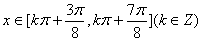 ,
,
即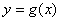 的单调减区间为
的单调减区间为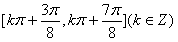 。
。
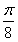 ,2)运动到相邻最低点时,函数图形与的交点的坐标为(
,2)运动到相邻最低点时,函数图形与的交点的坐标为(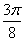 ,0),
,0), ∴
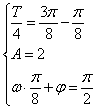 ,
,从而
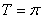 ,
,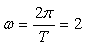 ,
,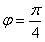 ,
,∴函数的解析式为
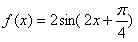 。
。(2)由(1)得
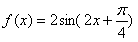 ,
,当
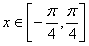 时,
时,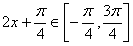 ,
,∴当
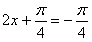 即
即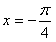 时,函数y取得最小值
时,函数y取得最小值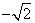 ,
,当
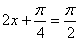 即
即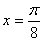 时,函数y取得最大值2。
时,函数y取得最大值2。(3)由题意,得
 ,即
,即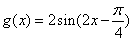 ,
,由
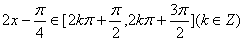 ,得
,得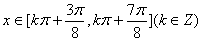 ,
,即
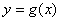 的单调减区间为
的单调减区间为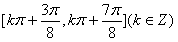 。
。
练习册系列答案
相关题目
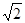 ),由最高点运动到相邻的最低点时,曲线与
),由最高点运动到相邻的最低点时,曲线与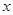 轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
轴交点E的坐标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.