题目内容
16.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为135°,则E的离心率为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\root{4}{2}$ |
分析 根据△ABM是顶角为135°的等腰三角形,得出|BM|=|AB|=2a,∠MBx=45°,进而求出点M的坐标,再将点M代入双曲线方程即可求出离心率.
解答 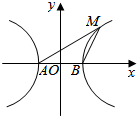 解:不妨取点M在第一象限,如右图:
解:不妨取点M在第一象限,如右图:
设双曲线的方程为:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),
∵△ABM是顶角为135°的等腰三角形,
∴|BM|=|AB|=2a,∠MBx=45°,
∴点M的坐标为(($\sqrt{2}$+1)a,$\sqrt{2}$a),
又∵点M在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$上,
∴将M坐标代入坐标得$\frac{(\sqrt{2}+1)^2a^2}{a^2}$-$\frac{2a^2}{b^2}$=1,
整理上式得,a2=(1+$\sqrt{2}$)b2,而c2=a2+b2=(2+$\sqrt{2}$)b2,
∴e2=$\frac{c^2}{a^2}$=$\sqrt{2}$,因此e=$\root{4}{2}$,
故选D.
点评 本题主要考查了双曲线的简单几何性质,灵活运用几何关系是解决本题的关键,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.已知函数f(x)=ax-1+logax在区间[1,2]上的最大值和最小值之和为a,则实数a为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
1.已知函数f(x)=sin(2x+φ)(0<φ<π),若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位后所得图象对应的函数为偶函数,则实数φ=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |