题目内容
6.已知f(x)为定义在R上的可导函数,下列命题:①若y=f(x)是奇函数,且在(0,+∞)上单调递增,则当x<0时,f(x)<0;
②若对任意的x>0,都有f(x)<f(0),则函数y=f(x)在[0,+∞)上一定是减函数;
③“函数y=|f(x)|的图象关于y轴对称”是“y=f(x)为奇函数”的必要不充分条件;
④若存在xi∈[a,b](1≤i≤n;n≥2;i,n∈N+),当x1<x2<x3<…<xn时,有f(x1)<f(x2)<f(x3)<…<f(xn),则函数y=f(x)在区间[a,b]上是单调递增;
⑤若?x0∈(a,b)使f′(x0)=0,且f′(a)f′(b)<0,则x=x0为函数y=f(x)的一个极值点.
其中正确命题的序号为①③⑤.
分析 ①由y=f(x)是奇函数,则f(0)=0,且在x∈(0,+∞)上单调递增,则在R上单调递增,即可判断出真假;
②不正确,例如取f(x)=$-\frac{1}{3}{x}^{3}+\frac{3}{2}{x}^{2}$-2x,f′(x)=-(x-1)(x-2),可知函数f(x)在x=2时取得极大值,f(2)=-$\frac{2}{3}$<0=f(0),即可判断出;
③若“y=f(x)为奇函数”,其图象关于原点对称,则“函数y=|f(x)|的图象关于y轴对称”;反之不成立,例如f(x)=x2,即可判断出真假;
④是假命题,例如取x∈[1,4],x∈[1,2)时,f(x)=$2(x-\frac{5}{4})^{2}+\frac{7}{8}$;x∈[2,3),f(x)=$-2(x-\frac{11}{4})^{2}$+$\frac{25}{8}$;x∈[3,4],f(x)=$2(x-\frac{13}{4})^{2}$+$\frac{23}{8}$,即可判断出真假;
⑤利用函数取得极值的充要条件即可判断出.
解答 解:①若y=f(x)是奇函数,则f(0)=0,且在x∈(0,+∞)上单调递增,由奇函数的性质可得:在R上单调递增,因此当x<0时,f(x)<f(0)=0,因此正确;
②若对任意的x>0,都有f(x)<f(0),则函数y=f(x)在[0,+∞)上一定是减函数,不正确,例如取f(x)=$-\frac{1}{3}{x}^{3}+\frac{3}{2}{x}^{2}$-2x,f′(x)=-(x-1)(x-2),可知函数f(x)在x=2时取得极大值,在x=1取得极小值,f(2)=-$\frac{2}{3}$<0=f(0);
③若“y=f(x)为奇函数”,其图象关于原点对称,则“函数y=|f(x)|的图象关于y轴对称”;反之不成立,例如f(x)=x2,函数y=|f(x)|=x2的图象关于y轴对称,是偶函数,因此正确;
④是假命题,例如取x∈[1,4],x∈[1,2)时,f(x)=$2(x-\frac{5}{4})^{2}+\frac{7}{8}$;x∈[2,3),f(x)=$-2(x-\frac{11}{4})^{2}$+$\frac{25}{8}$;x∈[3,4],f(x)=$2(x-\frac{13}{4})^{2}$+$\frac{23}{8}$,满足f(1)<f(2)<f(3)<f(4),但不是单调递增函数.
⑤若?x0∈(a,b)使f′(x0)=0,且f′(a)f′(b)<0,则x=x0为函数y=f(x)的一个极值点,正确.
故答案为:①③⑤.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | 0 | B. | 1 | C. | 15 | D. | -15 |
| A. | -26 | B. | 26 | C. | -10 | D. | 10 |
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\root{4}{2}$ |
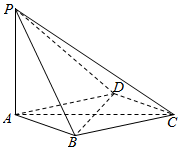 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°. 如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.