题目内容
已知函数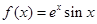 .
.
⑴ 求函数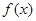 的单调区间;
的单调区间;
⑵ 如果对于任意的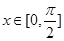 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
⑶ 是否存在正实数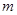 ,使得:当
,使得:当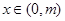 时,不等式
时,不等式 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.
(1)
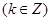 .;(2)
.;(2)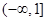 ⑶详见解析.
⑶详见解析.
解析试题分析:(1)利用求导的基本思路求解,注意导数的四则运算;(2)利用转化思想将问题转化为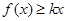 总成立,只需
总成立,只需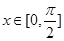 时
时 .借助求导,研究
.借助求导,研究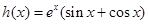 的性质,通过对参数k的讨论和单调性的分析探求实数
的性质,通过对参数k的讨论和单调性的分析探求实数 的取值范围;⑶通过构造函数和等价转化思想,将问题转化为
的取值范围;⑶通过构造函数和等价转化思想,将问题转化为 ,要使
,要使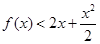 在
在 上恒成立,只需
上恒成立,只需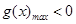 .然后利用求导研究函数的最大值,进而证明结论.
.然后利用求导研究函数的最大值,进而证明结论.
试题解析::(1) 由于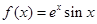 ,
,
所以 . (2分)
. (2分)
当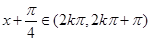 ,即
,即 时,
时, ;
;
当 ,即
,即 时,
时,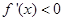 .
.
所以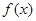 的单调递增区间为
的单调递增区间为
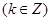 ,
,
单调递减区间为
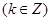 . (4分)
. (4分)
(2) 令 ,要使
,要使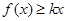 总成立,只需
总成立,只需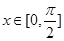 时
时 .
.
对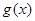 求导得
求导得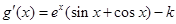 ,
,
令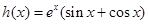 ,则
,则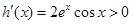 ,(
,(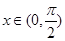 )
)
所以 在
在 上为增函数,所以
上为增函数,所以 . (6分)
. (6分)
对 分类讨论:
分类讨论:
① 当 时,
时, 恒成立,所以
恒成立,所以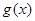 在
在 上为增函数,所以
上为增函数,所以 ,即
,即 恒成立;
恒成立;
② 当 时,
时,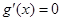 在上有实根
在上有实根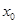 ,因为
,因为 在
在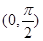 上为增函数,所以当
上为增函数,所以当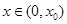 时,
时, ,所以
,所以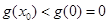 ,不符合题意;
,不符合题意;
③ 当 时,
时, 恒成立,所以
恒成立,所以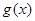 在
在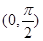 上为减函数,则
上为减函数,则 ,不符合题意.
,不符合题意.
综合①②③可得,所求的实数 的取值范围是
的取值范围是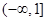 . (9分)
. (9分)
(3) 存在正实数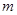 使得当
使得当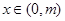 时,不等式
时,不等式 恒成立.
恒成立.
理由如下:令 ,要使
,要使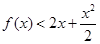 在
在 上恒成立,只需
上恒成立,只需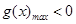 . &
. &

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 ,
, 为函数
为函数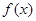 的导函数.
的导函数.  ,求
,求 的值;
的值; ,求函数
,求函数 的单调区间.
的单调区间. (
( 是自然对数的底数).
是自然对数的底数). 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值; 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与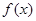 在
在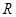 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.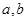 是实数,函数
是实数,函数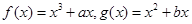 ,
,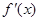 和
和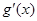 ,分别是
,分别是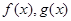 的导函数,若
的导函数,若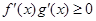 在区间
在区间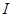 上恒成立,则称
上恒成立,则称 和
和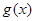 在区间
在区间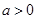 ,若函数
,若函数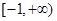 上单调性一致,求实数
上单调性一致,求实数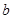 的取值范围;
的取值范围;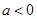 且
且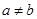 ,若函数
,若函数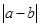 的最大值.
的最大值. .
.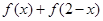 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;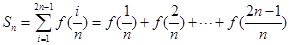 ,其中
,其中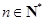 ,求
,求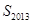 ;
;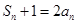 .若不等式
.若不等式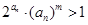 对
对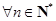 且
且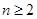 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 (
( )成立,求实数
)成立,求实数 .
.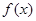 的单调区间;
的单调区间;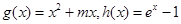 ,若在
,若在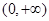 上至少存在一点
上至少存在一点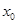 ,使得
,使得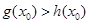 成立,求
成立,求 的范围.
的范围.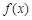 是定义在
是定义在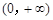 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记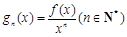 .若对定义域内的每一个
.若对定义域内的每一个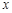 ,总有
,总有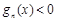 ,则称
,则称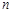 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个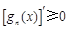 ,
,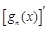 为函数
为函数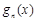 的导函数).
的导函数). 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数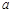 的取值范围;
的取值范围;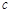 ,使得
,使得 恒成立,试判断
恒成立,试判断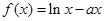 ,
,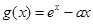 ,其中
,其中 为实数.
为实数. 在
在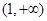 上是单调减函数,且
上是单调减函数,且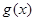 在
在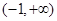 上是单调增函数,试求
上是单调增函数,试求